All published articles of this journal are available on ScienceDirect.
Fuzzy String Matching Procedure
Abstract
Background:
There are different methodologies for DNA comparison based on two string algorithms, which are dependent on crisp logical principles, where there is no room for verbal (linguistic) uncertainty. These are successfully applicable procedures in DNA bioinformatics researches even by taking into consideration probabilistic random variability components based on the probability distribution functions of various types.
Objective:
The main purpose of this paper is to review first briefly all available DNA string matching methodologies that are based on crisp logic and then to suggest a new method based on the fuzzy logic rules and application.
Methods:
There are different methodologies for DNA comparison based on two string algorithms, which are dependent on crisp logical principles, where there is no room for verbal (linguistic) uncertainty. These are successfully applicable procedures in DNA bioinformatics researchers even by taking into consideration probabilistic random variability components based on the probability distribution functions of various types.
Results:
Fuzzy number representation of each gene implies some sort of uncertainty or unhealthiness in some or all the genes. Their better identifications can be achieved on the basis of fuzzy numbers with different membership degrees, which imply the unhealthiness or healthiness of the genes and their collective behaviors.
Conclusion:
After the development of fuzzy number representation of the text string coupled with crisp pattern string their relationships are searched at different shift operations, and hence, the possibility of defaulters are identified in the text string with a certain degree of membership.
1. INTRODUCTION
Informatics procedures are employed in various disciplines for string pattern identification including biology, genetic works, computer sciences, engineering, medicine, etc. The main idea is to match two parallel strings composed of different and alike numerical or symbolic bits of different sizes. Such methodologies are used frequently in DNA researches.
There are various works on the crisp string matching procedure in the literature, where the most widely used three algorithms are the classical Nhaive, Morris-Pratt, and Knuth-Morris-Pratt methodologies.
Alsmadi and Nuser [1] based their work for DNA comparison on two popular string algorithms as the longest common substring, and subsequence by means of a two-string match, but they reached to the conclusion that their implementations are not consistent through research papers or websites that use and implement those algorithms for DNA sequence comparison. Nsira et al. [2] tackled online exact string matching to a pattern in a set of highly similar sequences. In this sentence “highly” implies a fuzzy word, which means that text sequence may not be crisply feasible, i.e., fuzzy to a certain extent. They have considered the application of two well-known string matching procedures, namely, the classical Morris-Pratt and Knuth-Morris-Pratt algorithms with error boundaries. Accordingly, they have modified these two algorithms by taking into consideration through the Hamming distance border calculations. However, they are still within the random error bans, but not within the fuzzy uncertainty domain, which is the main purpose of this paper.
Along the uncertainty lines, Huang et al. [3] have proposed an assumption-based solution about the DNA string as common segments and non-common segments in two parts, which implies two clusters that are neither exactly crisp nor fuzzy. Perhaps their division can be visualized as 50% each or any two percentages that add up to 100%. Such an approach significantly reduces the memory allocation with fast string match, but it is restrictive as to similar sequence type specification. A procedure is suggested for string matching based on querying highly similar structured sequences via binary encoding and word level operations [4]. A similar approach has been provided by storing the entire reference string with a difference in the next string [3].
Some researchers have analyzed matching results for arriving at a more efficient string match algorithm, and for this purpose, they have used three algorithms and came out with the conclusion that the Boyer Moore algorithm is faster and efficient for matching large DNA sequences. The comparison result also demonstrated that the matching values of natural genomes are higher than virus genomes [5].
A detailed account of fuzzy logic applications in the bioinformatics and computer biology domains is given in a textbook by Xu et al. [6], where they stated that the superior capability of fuzzy logic as a modeling language is one of the principal rationales for its use in bioinformatics, and more generally, in scientific theories. The principles of fuzzy logic and its inference procedures have much to do and support bioinformatics problems such as string match algorithm, which is touched upon in this paper. Compared to fuzzy logic rules, the crisp logic and probability theory have less informatics information with their non-elastic boundary conditions. In the literature, there are rare publications about the application of fuzzy logic principles to bioinformatics and computer sciences. The biological systems have uncertainties that cannot be expressed only by numbers, but by words like “similar”, “rather”, “random”, “highly”, “low”, and “like”, which are different than numerical uncertainty. On the other hand, exact and various optimization methods have crisp limitations in bioinformatics string match algorithms.
In all the above mentioned procedural applications both strings (text and pattern) are considered as crisp existences without any damage. Although mutation is available, it is crisp. In this paper, two types of bluntness, in other words, as in the literature fuzzy bits and genes are taken into consideration as the first fuzzification and the next one is the shifting fuzziness in the text string, which may be pathological to a certain extent, but the pattern (control) string is assumed as crisp similar to the literature. Under these circumstances, the final match result will not be a crisp number, but a fuzzy membership degree (MD) between 0 and 1, inclusive. The closer is the MD to one, the better and healthy is the text string. The suggested fuzzy string match algorithm is more effective than the previous alternatives as for the reality is concerned, and also from much faster search point of view on-line crisp or probabilistic string matching algorithm.
2. METHODS
2.1. Classical Matching Procedures
There are several methodological string match procedures in the literature from the simplest one, which requires longer time durations for execution in the computer than others. The list of existing string match procedures is presented in Table 1.
The Smith-Waterman [15] algorithm is a classical tool for the identification and quantification of local similarities in biological sequences. The algorithm demonstrates empirical evidence of practicality and the efficiency gains. Their algorithm provides local similarity quantification between two different biological strings. This algorithm is in extensive use for finding near-matches in a good manner in biological sequences, and it is referred to as the local alignments identifier [19].
The string match algorithm identifies all occurrence probabilities of a pattern in a given text [14]. This can be employed for single and multiple pattern matching procedures. Its major areas of application are mostly in plagiarism and DNA sequences matching.
An efficient string match algorithm is suggested for two biological sequences comparisons through dynamic programming [17]. Through the comparison procedure, the Brute-Force algorithm searches the given pattern within the text by shifting one character at a time until non-matching characters are identified.
Fuzzy logic rule base and inference have been used in much less extent in the bioinformatics than the algorithms mentioned in Table 1. It is, therefore, possible to fuzzify some of the classical string match algorithms, which is the main purpose of this paper.
2.2. Fuzzy String Fundamentals
The data in the bioinformatics domains are not only rich but have “heterogeneous” natural features in addition to “random noise”, “incompleteness” and “outliers” that may cause to misleading and misunderstanding of the modeling outputs. Each one of the words in quotation marks has fuzzy content with numerical implications. On the other hand, evolution, adaptability, redundancy, robustness, and emergency provide extremely complex systems, which can be dealt with fuzzy logic principles. Biological data treatments cannot be tackled by a single specialization but need a team of different disciplines. In this case, the linguistic terminology becomes the most important problem initially, which should be settled among the research groups, so that they can understand the common problem linguistically, i.e. by verbal information, which is the basis of the fuzzy logical principles. A common linguistic understanding includes many logically rational predicates that are the fundamentals of mathematical expressions, algorithmic developments and sustainable advancement in the bioinformatics problem solutions.
It is stated that “As a simple illustration, consider the problem of classifying new genes by their DNA sequences [6]. Sequencing machines actually produce memberships (or probabilities) for all four DNA bases (A, C, T, and G) at each position. Most of the time, the nucleic acid with the highest membership is chosen, and from that point on, the sequence is treated as if it were deterministic. Hence, potentially valuable information is discarded and unavailable in subsequent processing. If this deterministic sequence is matched to a database and, say, only the top match is considered, additional information is lost. This statement validates the employment of fuzzy concepts, logic, rules, numbers and inferences in the bioinformatics problem solutions. Furthermore, for appre ciation of problem fundamentals linguistically, one needs to ponder on science philosophical and logical aspects for better algorithm developments with a critical review of the available ones [20].
In general, deterministic string match problems are based on two sequences (strands), which the text, T, with n elements more than the pattern, P, sequence element number, m, (m < n). The problem is under the assumption that each one of the genes in these strands is healthy without any ambiguity, incom pleteness, vagueness and bluntness. In this case, each one will have crisp and complete information, which means that no uncertainty ingredient exists in their structure. Each gene within the text strand can be attached with different fuzzy sets as membership functions in the form of fuzzy numbers, which have been assumed in this paper in triangular shapes. As for the pattern strand, there is no fuzziness in its elements, but its position may have some uncertainty along with the matching procedure, and hence, there may be a slight diff erence in its location in cases of a match, which implies fuzzy matching. The deterministic T and P structural locations are given as follows.
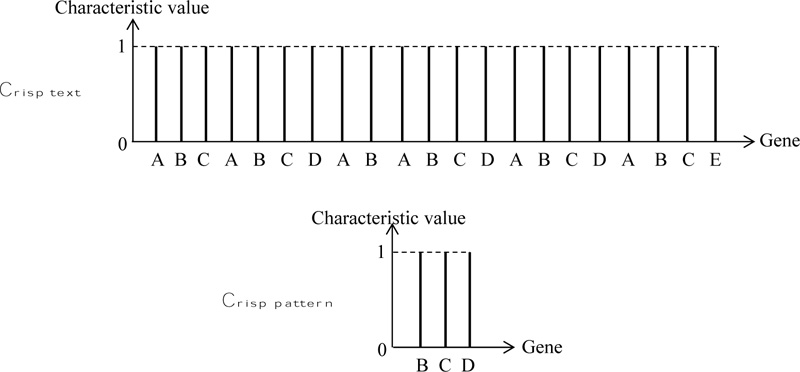
T, (Text): ABCABCDABABCDABCDABDE
P, (Pattern): BCD
In these two strands, there are five different genes, A, B, C, D, and E each with crisp information without any sort of numerical or verbal uncertainty. Their numerical representation can be achieved by digits, say like 1, 2, 3, 4 and 5, respectively.
T, (Text): 123123412123412341245
P, (Pattern): 234
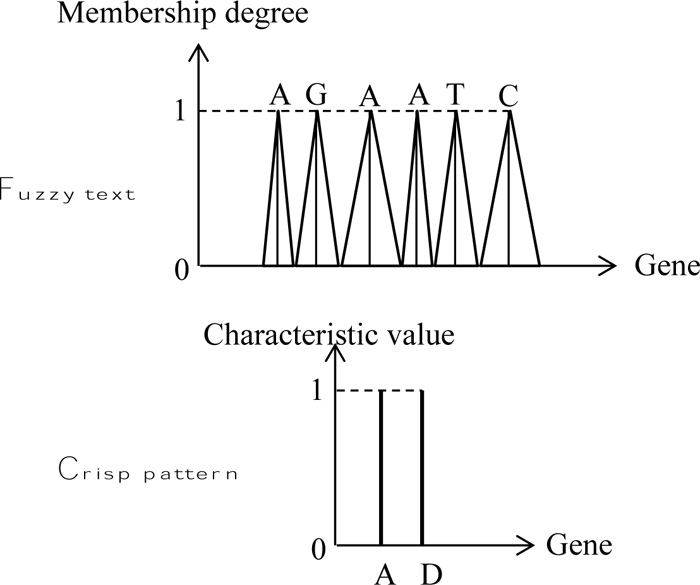
According to the crisp logical sequencing, each one of these letters or number symbols can be written with their characteristic value (similar to the membership degree), which is always equal to one as in Fig. (1).
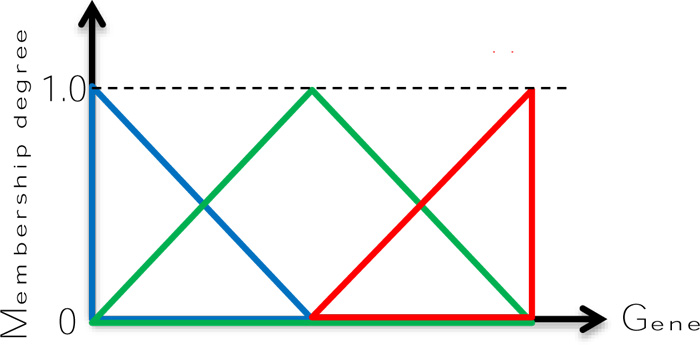
Zadeh [21-26] suggested the use of fuzzy sets for uncertain words with their membership functions (MFs), and then onwards the fuzzy logic consciousness has developed in different disciplines. MFs are the source of common sense and expert view appreciations depending on linguistic expression conveyance from heuristics and questionnaires and alike. The simplest fuzzy MFs are given in Fig. (2) as “Low”, “Medium” and “High”.
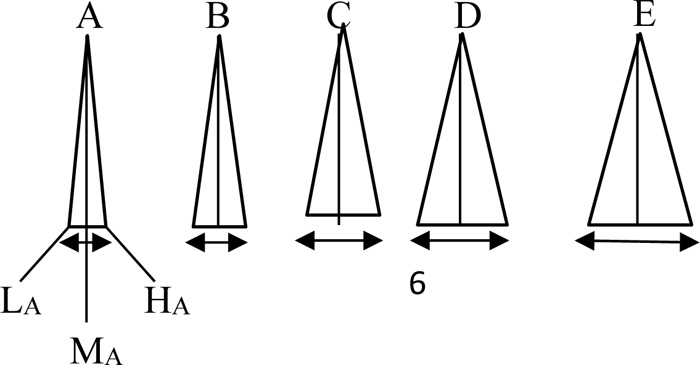
In the case of fuzzy logic and set for each gene instead of crisp numbers, the fuzzy numbers in Fig. (3) can be substituted for a fuzzy strand match algorithm.
Each one of these fuzzy numbers has at the base three crisp values as “Low”, “Medium”, and “High”. Accordingly, depen ding on the letters, these fuzzy labels can be shown notationally, say, for A as LA, MA, and HA, and for other letters, the subscripts take their forms. In Fig. (4), the text string is considered as fuzzy, but the pattern is still in script forms
Fig. (5) presents both text and pattern strings in the form of fuzzy numbers with different base lengths for “Low”, “Medium”, and “High” values.
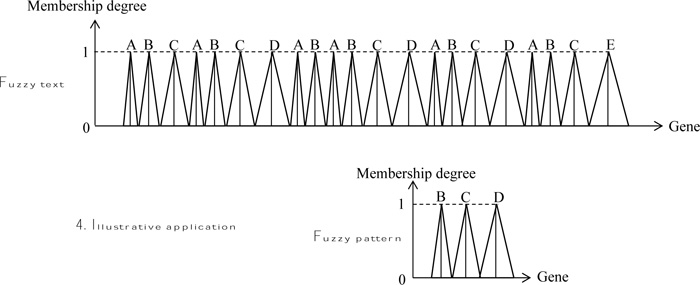
2.3. Illustrative Application
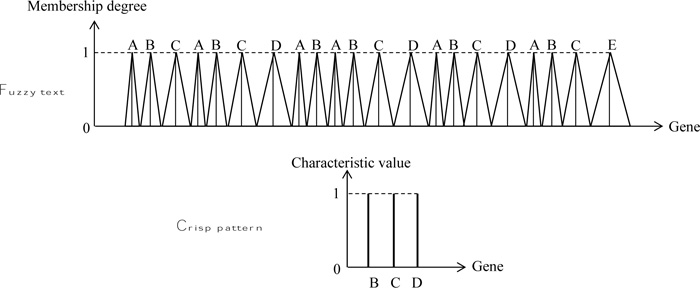
In order to indicate the application of fuzzy text and pattern match algorithm, herein, rather simple patterns are adapted as in many basic documents. The execution is performed through the naive string matcher in a DNA string as in Fig. (6), where the text sequence is assumed as fuzzy, but the pattern string is without fuzziness. The solution position is given in Fig. (7).
This figure presents the different features of fuzzy text search correspondence to the crisp pattern strand. The fol lowing points are important for the identification of crisp patterns match to the fuzzy text as shown in the same figure by means of three cases.
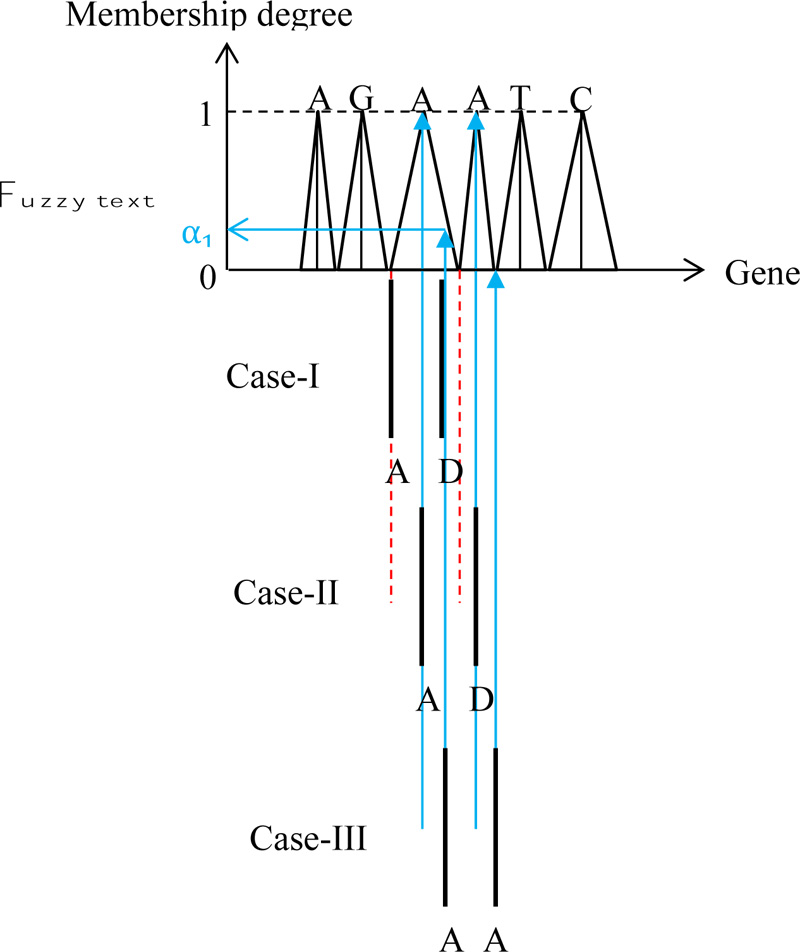
1) During pattern shifting operation even though the crisp gene on the right-hand side enters the A gene in the text, there is no match until the two A genes enter the domain of AA genes in the text strand,
2) Case-I: Even though the two crisp pattern elements are within the domain of text strand, but since both of them are within the first A gene, there is no match yet between the text and pattern strands, because both pattern genes are within the first A gene influence,
3) Case-II: Its range corresponds with the maximum MD equal to 1 in one of the text gene, and the other with 0 MD in the next gene, which does not provide fuzzy interference. However, one can consider it as the crisp logic solution, where the characteristic value (or MD) is equal to 1.
4) Case-III: The pattern string correspondence with the text provides an MD value as α1 Fig. (7).
Although herein, three cases are explained, there are many cases among these three, and hence, the reader can develop his/her view depending on the expert view, which one to adapt for the final solution.
3. RESULTS AND DISCUSSION
Bioinformatics string match algorithms provide a wide range of applications, especially, in biology and computer information for the identification of a given pattern to match a basic text string. In the literature, almost in all cases, both text and pattern strings are taken as crisp values, which is based on two-valued (0 and 1) crisp logic. In this paper, various versions of fuzzy logic alternatives are explained, and an illustrative example solution is provided by considering verbal uncertainty, i.e., fuzzy text match possibility with the crisp pattern string.
It is suggested in this paper that the fuzzy logic rules and inference systems must be cared for the bioinformatics applications. Fuzzy number representation of each gene implies some sort of uncertainty or unhealthiness in some or all the genes. Their better identifications can be achieved on the basis of fuzzy numbers with different membership degrees, which imply the unhealthiness or healthiness of the genes and their collective behaviors.
CONCLUSION
One can discuss that fuzzy string match is a general approach with its membership function and degrees, which provide information as to the partial belongingness rather than clear cut two-valued crisp logic, where one is not able to deal with uncertainties and especially with linguistic uncertainties. The crisp logic algorithms may treat the numerical uncertainty sources probabilistically, but fuzzy logic inference subsumes both uncertainty types. It is recommended that the role of fuzzy logic in the gene network modeling should be further explored in string-matching algorithms for better conclusive presentations than the probabilistic approaches.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


