A Study on the Relevance of Feature Selection Methods in Microarray Data
Abstract
Background:
This paper studies the relevance of feature selection algorithms in microarray data for effective analysis. With no loss of generality, we present a list of feature selection algorithms and propose a generic categorizing framework that systematically groups algorithms into categories. The generic categorizing framework is based on search strategies and evaluation criteria. Further, it provides guidelines for selecting feature selection algorithms in general and in specific to the context of this study. In the context of microarray data analysis, the feature selection algorithms are classified into soft and non-soft computing categories. Their performance analysis with respect to microarray data analysis has been presented.
Conclusion:
We summarize this study by highlighting pointers to recent trends and challenges of feature selection research and development in microarray data.
1. INTRODUCTION
Microarray data is a high throughput technology used in cancer research for diagnosis and prognosis of disease [1]. It offers the ability to simultaneously measure thousands of gene expression values. The microarray data analysis is structured, based on basic four steps: First, the raw data generated from the instruments need to be imported and parsed using specific libraries. Secondly, such data are preprocessed partially eliminating the noise, and data are annotated with biological information stored in specific libraries. Finally, data-mining algorithms extract biological information from annotated data [2]. DNA microarray data, which provides gene expression values, can be used for prediction of disease outcome, classification of cancer types and identification of relevant genes [3]. Since Microarray data consists of hundreds of thousands of features in comparison to the number of samples, it undergoes the curse of dimensionality problem. However, a very small number of features contribute to the classifier or which is relevant to an outcome of interest. For example, one or two genes behavior may be responsible for a particular cancer type such as p53 which act as a biomarker in Lung cancer dataset and expressed differentially so instead of taking the uncorrelated genes with the biomarker we should make a subset of correlated genes which can give accurate classification accuracy. Thus, effective feature selection techniques are often needed in this case to aid to correctly classify different tumor types and consequently lead to a better understanding of genetic signatures as well as improve treatment strategies [4].
A feature in a dataset is an individual measurable property of the process being observed [5]. The feature (gene) selection process helps in understanding data, reducing computational requirement, reducing the effect of the curse of dimensionality and improving the performance of the classifier. The process of removing irrelevant, noisy and redundant features and finding the relevant feature subset based on which the learning algorithm improves its performance is known as feature selection. Feature selection is primarily applied on the dataset comprises of thousands of features with small sample size (e.g., microarray data). Where feature selection is termed as gene selection or Biomarker selection. The intentions of feature selection are manifold: some of the important objectives are first to exclude overfitting and enhance model performance i.e., prediction accuracy in the case of supervised classification and better cluster detection in the case of clustering. Second, to provide faster and better cost-effective models and third to gain a deeper insight into the underlying processes that generated the data [6]. Instead of the conventional method of feature selection, soft computing techniques (i.e. fuzzy logic, neural networks, and evolutionary algorithms) are also applied for feature selection on high dimensional data. In this case, the high dimensional dataset is converted into low dimensional dataset by selecting an optimal number of genes. To accomplish the optimal gene selection process, several evolutionary algorithms are widely used for high dimensional dataset such as genetic algorithm, ant colony optimization algorithm, particle optimization algorithm etc. Feature selection is a complex process in high dimensional data set as there is multifarious interaction among features for large search space. Therefore, exhaustive search technique is quite unfeasible for these situations. To resolve this issue conventional searching techniques are used such as sequential forward selection and sequential backward selection. However, these search techniques suffer from stagnation in local optima and high computational cost. In order to address the issues in the above searching techniques, global search methods like evolutionary algorithms are used. In genetic algorithm an evolutionary search using genetic operators combined with a fitness function searches and evaluates the selected features to get the optimal feature subset. Feature selection process in ant colony optimization is a pathfinding problem. Where the ants lay pheromone along the edges of the graph and the traces get thicker when the path leads towards the optimal path (optimal features). Particle swarm optimization adapts a random search strategy for feature selection. The particles move in a multidimensional space attracted towards the global best position. The movement of the particles is influenced by the previous experience and by other particles and this approach is used for feature selection. These evolutionary algorithms are associated with many hybrid approaches for reducing the number of features. The current study presents the fundamental taxonomy of feature selection, along with reviews the consortium of state-of-the-art feature selection methods present in the literature into two categories: non soft computing and soft computing approach of feature selection.
The rest of the paper is set out as follows. Section 2, describes the objective of feature selection and its relevance for model generation. Section 3, discusses the steps of feature selection and categorization of the algorithms into soft and non-soft computing methods along with their performance analysis. Section 4, deals with the feature selection methods used for microarray data. Section 5, highlights pointers to recent trends and challenges in feature selection.
2. FEATURE SELECTION AND ITS RELEVANCE
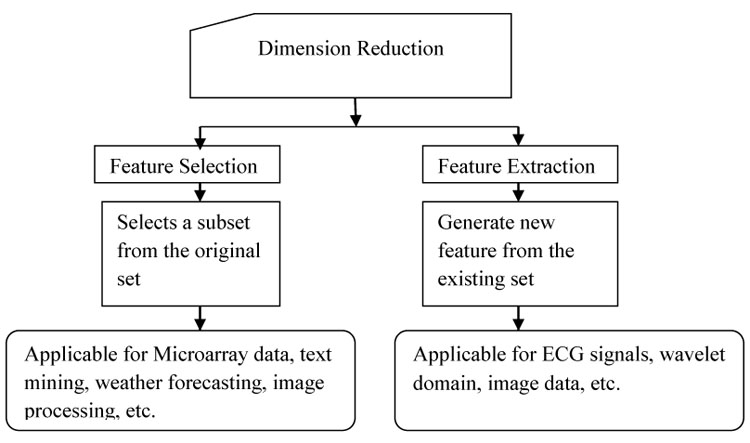
Traditionally manual management of the high dimensional data set is more challenging. With the advent of data mining and machine learning techniques, knowledge discovery and recognition of patterns from these data can be done automatically [7]. However, the data in the database is filled with a high level of noise and redundancy. One of the reasons causing noise in these data is an imperfection in the technologies that collected the data and the source of the data itself is another reason. Dimensionality reduction is one of the famous techniques to remove noisy (i.e. irrelevant) and redundant features. For data mining techniques such as classification and clustering dimensionality reduction is treated as preprocessing task for better performance of the model. Dimensionality reduction techniques can be classified mainly into feature extraction and feature selection. Feature extraction approaches set features into a new feature space with lower dimensionality and the newly constructed features are usually combinations of original features. On the other hand, the objective of feature selection approaches is to select a subset of features that minimize redundancy and maximize relevance to the target such as the class labels in classification. Therefore, both feature extraction and feature selection are capable of improving learning performance, lowering computational complexity, building better-generalized models, and decreasing required storage. Fig. (1) shows the classification of dimension reduction process and the data set in which these are generally applied in the literature. Feature selection selects a group of features from the original feature set without any changeover and maintains the physical meanings of the original features. Therefore, feature selection is superior in terms of better readability and interpretability [8, 9]. One of the applications would be in gene microarray data analysis [10-14]. Feature selection has its significance in many real-world applications such as finding relevant genes to a specific disease in Microarray data, analysis of written text, and analysis of medical images, analysis of the image for face recognition and for weather forecasting.
There are a number of different definitions in the machine learning literature for relevant feature selection. The feature is relevant which correlate to the target concept. The target concept (tc) depends upon the problem and the requirement. So, the simplest conviction of relevance is a perception of being “relevant to the tc”.
Definition 1: (Relevant to the target): A feature xi is relevant to a target concept (tc) if there exists a pair of examples A and B in the instance space such that A and B differ only in their assignment to x and tc(A)! = tc(B).
Definition 2: (Strongly Relevant to the sample)
A feature xi is strongly relevant to sample S if their present examples A and B in S differ only in their assignment to x and have different labels (or have several distributions of labels if they appear in S multiple times). Similarly, x is highly relevant to tc and distribution D if there exist examples A and B having non-zero probability over D that differ only in their assignment to x and satisfy tc(A)!=tc(B).
Definition 3: (Weakly Relevant to the sample):
A feature xi is weakly relevant to sample S (or target tc and distribution D) if there is a possibility of removal of a subset of the features so that xi becomes strongly relevant.
Definition 4: (Relevance as a complexity measure)
Given a paper of data D and a set of concept C, let r (D, C) be the number of features relevant using Definition 1 to a concept in C that out of all those whose error over D is least, has the fewest relevant features.
In this article different existing FS methods defined by many others are universal and compared. The subsequent list which is theoretically different and covers up a variety of definitions are given below.
General Definition: A large set of (D) items is given from which we need to find a small subset (d) being optimal in a certain sense [15].
Generic Definition: FS consists of identifying the set of features whose expression levels are indicated to a particular target feature (clinical/biological annotation). Mathematically, this problem can be viewed as follows: Let
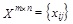 be a matrix containing‘m’ features and ‘n’ samples generating from different groups started by a target annotation. Selection of the most informative genes consists of identifying the subset of genes across the entire population of samples
be a matrix containing‘m’ features and ‘n’ samples generating from different groups started by a target annotation. Selection of the most informative genes consists of identifying the subset of genes across the entire population of samples
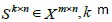 which are the most discriminative for the outlined classes. This definition is only valid for classification problems where the groups are clearly identified beforehand [16].
which are the most discriminative for the outlined classes. This definition is only valid for classification problems where the groups are clearly identified beforehand [16].
2.1. Feature Selection based on Relevance and Redundancy
Relevance definitions divide features into three categories such as strongly relevant, weakly relevant and irrelevant features. Redundancy definition further divides weakly relevant features into redundant and non-redundant ones. Relevance analysis determines the subset of relevant features by removing the irrelevant ones, and redundancy analysis determines and eliminates redundant features from relevant ones and thus produces the final subset [12].
Idealized: uncover the minimally sized feature subset that is necessary and sufficient to the target concept [17].
Classical: choose M features from a set of N features (where M < N), such that the value of a criterion function is optimized over all subsets of size M [18].
2.2. Improving Prediction Accuracy
The objective of feature selection is to improve the prediction ability of the classifier by reducing the structure size. The final training feature subset is constructed using the selected features only [19].
3. FEATURE SELECTION STAGES AND CLASSIFICATIONS
There are four basic stages in feature selection method: (i) Generation Procedure (GP), to select candidate feature subset (ii) Evaluation Procedure (EP), to evaluate the generated candidate feature subset and output, a relevancy value (iii) Stopping Criteria (SC): To determine when to stop (iv) Validation Procedure (VP): To determine whether it is the optimal feature subset or not. The process of feature selection approach is given in (Fig. 2).
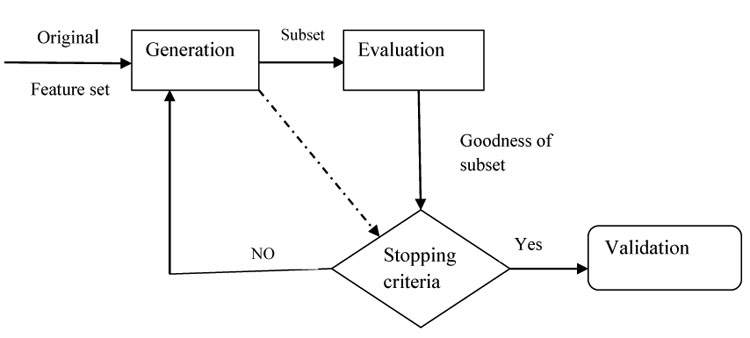
3.1. Generation Procedure (GP)
This procedure generates a subset of features that is relevant to the target concept. GP are of two types
3.1.1. Individual Ranking
Measures the relevance of each feature. The feature relevance is measured based on some evaluation function. In this case, each individual feature is evaluated by assigning some weight or score.
3.1.2. Subset Selection
A subset of features is selected based on some search strategy. If the size of the data set is N×M, then a total number of features in the data set is N. The possible number of subsets of features is 2N. This is even very large for a medium sized feature set. Therefore suitable search strategy is applied to this process. The search is classified as:
A. Complete: It traverses all the feasible solutions. This procedure does an exhaustive search for the best possible subset pertaining to the evaluation function. Example of complete search is a branch and bound best first search.
B Heuristic Deterministic: uses a greedy strategy to select features according to local change. There are many alternatives to this straightforward method, but the creation of subset is basically incremental. Examples of this procedure are sequential forward selection, sequential backward selection, sequential floating forward selection, and sequential floating backward selection.
C. Nondeterministic (Random): It attempts to find an optimal solution in a random fashion. This procedure is new in the field of feature selection methods compared to the above two categories. Optimality of the selected subset depends on the resources available.
3.2. Evaluation Procedure (EP)
An optimal subset is always relative to a certain evaluation function. An evaluation function tries to measure the discriminating ability of a feature or a subset to distinguish the different class labels. The evaluation function is categorized as distance, information (or uncertainty), dependence, consistency, and classifier error rate [25, 26].
3.2.1. Distance Measures
For a two-class problem say A and B are two features, then A and B are selected on the basis of their distance (e.g. Euclidian distance). If the distance is zero then the features are said to be redundant and ignored. The higher the distance the more the features are discriminating.
3.2.2. Information Measures
This determines the information gain for the feature. Feature A is preferred over feature B if the information gain of A is more than B (e.g. entropy measure).
3.2.3. Dependence Measures
Dependence or correlations of the ability to predict the value of one variable from the value of another. If the correlation of feature A with class C is higher than the correlation of feature B with class C then feature A is preferred to B.
This measure finds the minimally sized subset that satisfies the acceptable inconsistency rate that is usually set by the user.
3.2.4. Consistency Measure
This measure finds the minimally sized subset that satisfies the acceptable inconsistency rate that is usually set by the user.
3.2.5. Classifier Error Rate
The evaluation function is the classifier itself. It measures the accuracy of the classifier for different subsets of feature set and measures the error rate for the different subset.
We have classified the feature selection method as non-soft computing based and soft computing based. Based on the generation procedure and evaluation function, the feature selection methods are classified, where the generation procedure and evaluation functions are two dimensions.
3.2.6. Stopping Criteria
It indicates the end of the process. Commonly used stopping criteria are: (i) When the search completes (ii) When some given bound (minimum number of features or a maximum number of iterations) is reached. (iii) When a subsequent addition (or deletion) of any feature does not produce a better subset and (iv) When a sufficiently good subset (e.g. a subset if its classification error rate is less than the allowable error rate for a given task) is selected.
Consulting Table 1, the feature selection approaches are primarily categorized as a filter, wrapper, and embedded method. Recently other feature selection methods are gaining popularity i.e., hybrid and ensemble methods (Fig. 3).
|
Generation Procedure (GP) |
Evaluation Function(EF) | ||||
|---|---|---|---|---|---|
| Distance | Information | Correlation | Consistency | Classifier error rate | |
| Heuristic | Filter approach | Wrapper approach | |||
| Complete | |||||
| Random | |||||
| Embedded approach (filter + wrapper) | |||||
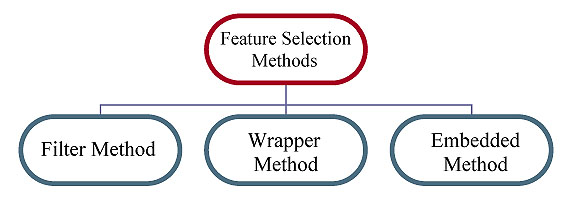
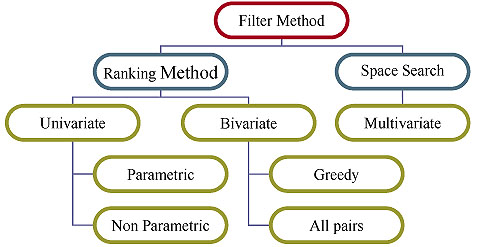
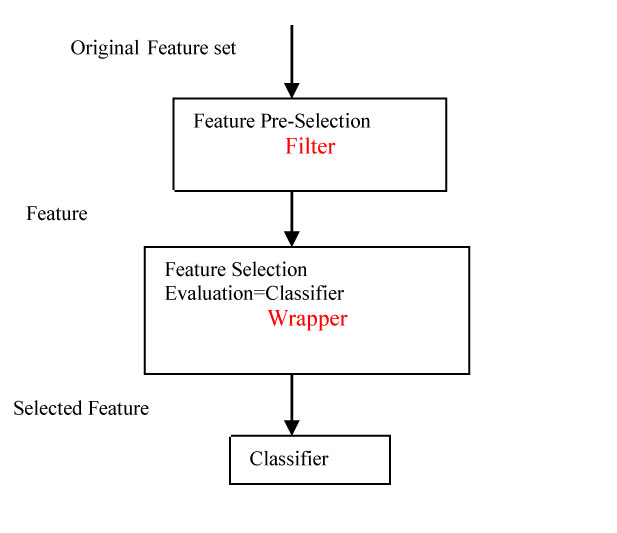
A. Filter Method
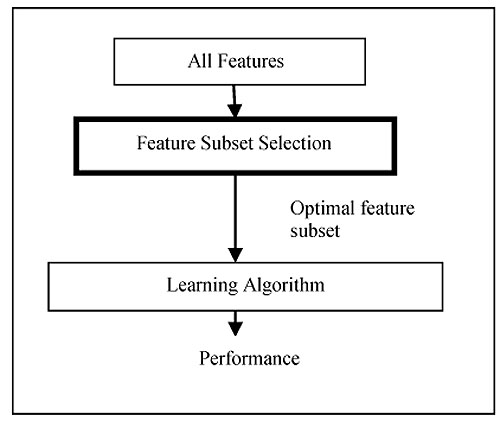
Filter method deals with individual ranking as well as subset selection. The individual ranking is based on the evaluation functions such as distance, information, dependence, and consistency excluding the classifier (Fig. 3). Filter techniques judge the relevance of genes by looking only at the intrinsic properties of the data. In microarray data, a gene relevance score is calculated, and low-scoring genes are removed. Afterward, this subset of genes is presented as input to the classification algorithm. The filtering technique can be used as a pre-processing step to reduce space dimensionality and overcome overfitting. The filter approach is commonly divided into two different sub-classes: individual evaluation and subset evaluation [20]. In individual evaluation method, the gene expression dataset is given as input. The method has an inbuilt evaluation process according to which a rank is provided to each individual gene based on which the selection is done. Different criteria can be adopted, like setting a threshold for the scores and selecting the genes which satisfy the threshold criteria, or sometimes the threshold can be chosen in such a way that a maximum number of genes can be selected. Then, the subset selected can be the final subset which is used as the input to the classifiers. In subset selection, all GP and evaluation function excluding the classifier can be taken for the combination. The model for the filter approach is given in Fig. (4).
However, methods in this framework may suffer from an inevitable problem, which is caused by searching through the possible feature subsets. The subset generation process usually increases the computational time but gives more relevant feature subset. In literature, it is found that the subset evaluation approach outperformed the ranking methods [19-22]. The filter method is again classified into the ranking method and space search method. Fig. (5), describes the taxonomy of filter feature selection method.
B. Wrapper Method
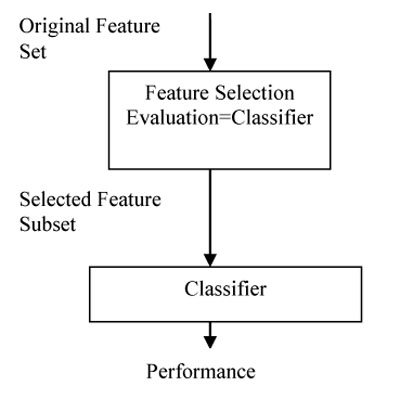
In the wrapper approach, all GP can be taken in combination with the classifier as evaluation function and generates the relevant feature subset. Wrappers are feedback methods, which incorporate the machine-learning algorithm in the feature selection process, i.e., they rely on the performance of a specific classifier to evaluate the quality of a set of features. Wrapper methods search through the space of feature subsets and calculate the estimated accuracy of a single learning algorithm for each feature that can be added to or removed from the feature subset. The search may be a GP and the evaluation function is a classifier. The model for the wrapper feature selection is given in Fig. (6). While building a wrapper algorithm one needs to find the answers for the following questions such as:
- How to find all possible feature subsets for evaluation?
- How to satisfy oneself with the classification performance of the chosen classifier in order to guide the search and what should be the stopping criteria?
- Which predictor to use?
The wrapper approach applies a blind search to find a subset of features. It searches randomly for the best subset which cannot be made sure without getting all possible subsets. Therefore, feature selection in this approach is NP-hard and the search with each iteration tends to become intractable for the user. This is not a preferred approach for feature selection, as it is a crude force method and requires higher computational time for feature subset selection.
The feature space in case of wrapper approach can be searched with various strategies, e.g., forward (i.e., by adding attributes to an initially empty set of attributes) or backward (i e., by starting with the full set and deleting attributes one at a time). The correctness of a specific subset of features/genes based on our classifier is obtained by training and testing the subset against that specific classification model.
The advantage of wrapper approach is that it selects a near perfect subset and error rate in this method is less as compared to other methods. The major disadvantage of the method is that it is computationally very intensive and it is intended for the particular learning machine on which it has been tested. Therefore, there is a high risk of overfitting than filter techniques.
The wrapper approach of feature selection is classified as sequential search based and Heuristic search based. The taxonomy of the wrapper model is given in Fig. (7).
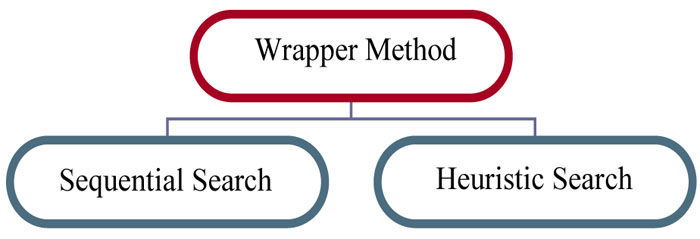
Usually, an exhaustive search is too expensive, and thus non-exhaustive, heuristic search techniques like genetic algorithms, greedy stepwise, best first or random search are often used. Here, feature selection occurs externally to the induction method using the method as a subroutine rather than as a post-processor. In this process, the induction algorithm is called for every subset of feature consequently inducing high computational cost [23, 24].
C. Embedded Method
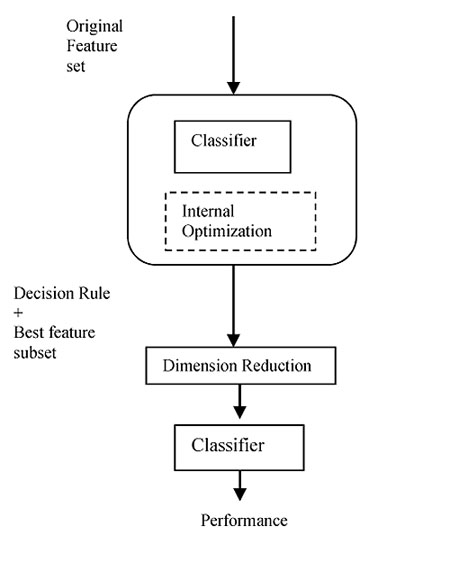
Despite the lower time consumption of the filter method, a major limitation of the filter approach is that it is independent of the classifier, usually resulting in worse performance than the wrappers. However, the wrapper model comes with an expensive computational cost, which is particularly aggravated by the high dimensionality of microarray data. An intermediate solution for researchers is the use of hybrid or embedded methods, which use the core of the classifier to establish criteria to rank features. Embedded methods are more tractable and efficient in comparison to wrapper approach. This method has a lower risk of overfitting compared to wrapper approach. Probably the most famous embedded method is Support Vector Machine based on Recursive Feature Elimination (SVM-RFE) [25]. Fig. (8), shows the schematic diagram of embedded feature selection Method.
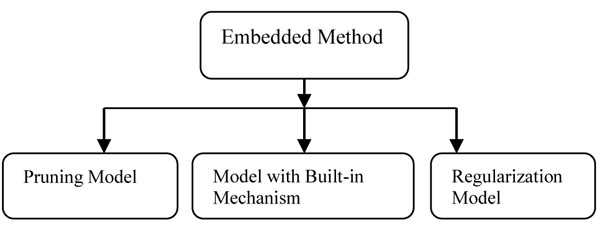
The embedded method is classified into three different categories. The taxonomy of embedded method is shown in Fig. (9).
D. Hybrid Method
It is the combination of any number of same or different classical methods of feature selection such as filter and wrapper methods. The combination can be a filter-filter, filter-wrapper, and filter-filter-wrapper where the gene subset obtained from one method is served as the input to another selection algorithm. Generally, filter is used to select the initial gene subset or help to remove redundant genes. Any combination of several filter techniques can be applied vertically to select the preliminary feature subset. In the next phase, the selected features are given to the wrapper method for the optimal feature selection. This method uses different evaluation criteria. Therefore, it manages to improve the efficiency and prediction accuracy with the better computational cost for high dimensional data. The most common hybrid method is mentioned in the paper [26] (Fig. 10).
E. Ensemble Method
Ensemble method is gaining popularity nowadays for feature selection in case of high dimensional data. This approach of feature selection produces a group of feature subset and either aggregated or intersected to produce the most relevant feature subset. This technique aggregates the significant features selected by different ranking approaches to formulate the most optimal feature subset. This method is therefore robust and stable while dealing with high dimensional data. A brief description of ensemble feature selection can be found in the paper [27] (Fig. 11).
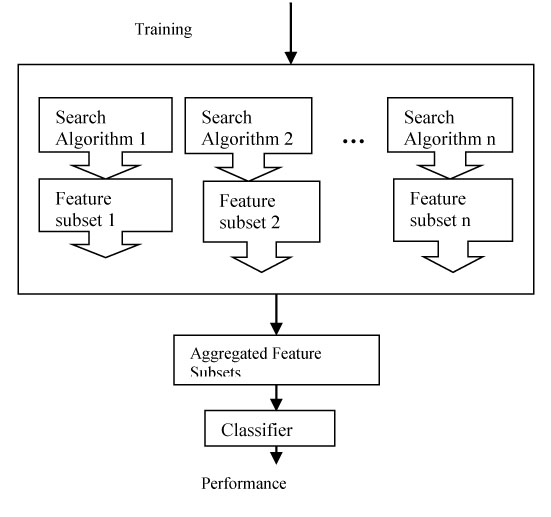
In this paper, we have classified the general feature selection approaches (filter wrapper and embedded) as non-soft computing approach and soft computing approach of feature selection.
3.3. Nonsoft Computing Methods of Feature Selection
All filter methods, some wrapper, embedded or hybrid methods are included in this category. Filter method ranks each feature according to some univariate metric keeping only the top-ranked features and eliminating low ranking features. There is no specific rule applied for the selection of the high ranking feature and elimination of the low ranking features. Some heuristic score is decided as high or low. Generally, it uses a scoring function to quantify the difference in expression between different groups of samples and rank features in decreasing order of the estimated scores. The topmost features are then selected as a good feature subset removing the others. Different categories of scoring functions for gene ranking are identified in the literature (Table 2).
| Scoring Function | Examples |
|---|---|
| Rank Score Family | 1.Wilcoxon rank sum [28] 2.Rank Product [29] |
| Fold Chain family | 1.Fold-change ratio [30] 2.Fold-change Difference [31] |
| t-Test family | 1.Z-score [32] 2.t-test [33] 3.Welch t-test [34] 4.Modified t-test [35-37] |
| Bayesian Family | 1.Bayesian t-test [38] 2.Regularised t-test [39] 3.Moderated t-test [40] 4.B-statics [41] |
| Information theory based Scoring family | 1.Info Gain [42] 2. Mutual info [43, 44] |
Univariate methods analyze a single variable whereas multivariate deal with more than one variable at a time. All filter individual ranking technique belongs to univariate methods and wrapper, embedded or hybrid methods belong to multivariate methods. Filter individual ranking univariate methods as well as bivariate methods are non-soft computing methods of feature selection (Table 3).
| Name of the Method | Parametric | Non-Parametric | |
|---|---|---|---|
| Univariate | ANOVA [94] | Y | N |
| Fold-change [91] | Y | N | |
| Regression model [92] | Y | N | |
| Regularized t-test [95] | Y | N | |
| Linear Model for Microarray Data(LIMMA) [96] | Y | N | |
| Gene ranking with B-statistics [97] | Y | N | |
| Gamma model [90, 93, 98, 120] | Y | N | |
| Signal to noise ratio [118] | Y | N | |
| Rank-sum [99] | N | Y | |
| Rank product [100] | N | Y | |
| Between-Within class Sum of Squares(BWSS) [101] | N | Y | |
| Relative entropy [102] | N | Y | |
| Threshold number of Misclassification(TnoM) [103] | N | Y | |
| Area Between the Curve and the Rising diagonal(ABCR) [104] | N | Y | |
| Significance Analysis of Microarray [105] | N | Y | |
| Empirical Bayes Analysis(EBA) [106] | N | Y | |
| Mixture Model Method(MMM) [107] | N | Y | |
| Bivariate | Greedy t-test [108] | Y | N |
| All pair t-test [108], | N | Y | |
| Top scoring pairs [109] | N | Y | |
| Uncorrelated Shrunken Centroid (USC) [110] | N | Y | |
| Multivariate | Correlation based Feature Selection(CFS) [111] | N | Y |
| Minimum Redundancy Maximum Relevance(MRMR) [112] | N | Y | |
| Markov Blanket Filter(MBF) [113] | N | Y | |
Wrapper FS technique uses subset generation strategy. It depends on the classifier to evaluate each subset. The subset generation process can happen in two different ways such as forward selection and backward elimination. First, the search starting point must be decided, which in turn influences the search direction. The search may start with an empty set and successively features can be added in the forward direction, or it may start with a full set and successively remove features i.e. elimination in the backward direction, or start with both ends and add and remove features simultaneously i.e. bidirectional. Non-soft computing Wrapper approaches of feature selections used in the literature are given below in (Table 4).
The embedded approach interacts with the learning algorithm at a lower computational cost than the wrapper approach. Feature dependencies are also captured by this method. It is not only the relationship between input features and the output feature but also searches features locally, which allows better local discrimination. It utilizes the independent criteria to choose the best subsets for a known cardinality. Then, the learning algorithm selects the ultimate optimal subset amongst the best possible subsets across different cardinality. The embedded subsets in soft computing methods in the literature are given in Table 5.
3.4. Soft computing Methods of Feature Selection
There are several soft computing methods of feature selection, which apply the subset generation strategy for feature selection or hybrid approach for feature selection. The search may also start with a randomly selected subset in order to avoid being trapped into local optima [27]. This search space is exponentially prohibitive for exhaustive search with even a moderate N. Therefore, different strategies have been explored: complete, sequential, and random search. These techniques use a dependency measure and a significant measure of a feature defined by rough, fuzzy set theory, soft set, Artificial Neural Network, Genetic algorithm, Particle Swarm Optimization, Ant Colony Optimization, metaheuristic optimization such as Bat algorithm etc. Further, the soft computing based feature selection approach is categorized into hybrid and nonhybrid approach (Tables 6 and 7).
| Method | Dataset |
Performance in % |
Number of Features Required in % |
|---|---|---|---|
| ANOVA [94] | Leukemia Ovarian Breast MULTMYEL Leukemia |
100 100 85 64 82 |
1 8 0.64 0.054 45.7 |
| Regression model [92] | Leukemia | 100 | 25 |
| Linear Model for Microarray Data(LIMMA) [96] |
Swirl ApoAI |
86 94 |
7.05 8.15 |
| Signal to noise ratio [119] | Leukemia Colon Lymphoma |
100 92.4 100 |
19.07 47.15 10.80 |
| Top scoring pairs [109] | Breast Leukemia Prostate |
79 94 95 |
2 5 2 |
| Correlation based Feature Selection(CFS) [111] |
Leukemia DLBCL |
78 95 |
14.15 11.02 |
| Name of the Method | Hybrid | Non-Hybrid | Key Idea |
|---|---|---|---|
| Signal feature extraction by Fuzzy Neural Network [45] |  |
– | ▪ The Approach combines the wavelet transform with fuzzy theory to improve the limitation of applying traditional fault diagnosis method to the diagnosis of multi-concurrent vibrant faults of aero-engine. |
| Rough set and weighted LS-SVM [46] |  |
– | ▪ A hybrid model, which combines rough set theory and least square support vector machine to forecast the agriculture irrigation water demand. |
| Artificial Neural Network in Agricology [47] | – |  |
▪ The survey was based on particular problem type, type of input, techniques used and results. |
| SNR-FFNN [51] | – |  |
▪ Comparison results of two approaches for selecting biomarkers from Leukemia dataset for feedforward neural network are given. ▪ The first approach implements k-means clustering and signal-to-noise ratio (SNR) for gene ranking, the top-scored genes from each cluster is selected and given to the classifiers. ▪ The second approach uses the signal to noise ratio ranking for feature selection. |
| Hybrid GA approach [48] |  |
– | ▪ The model accommodates multiple feature selection criteria. ▪ Find a small subset of feature that performs well for a particular inductive learning algorithm of interest to build the classifier. ▪ The subset selection criteria used are entropy-based feature ranking, t-statistics, SVM-Ref, GA as induction algorithm. |
| SNR-PSO [49] |  |
– | ▪ The proposed method is divided into two stages, ▪ The first stage uses k-means clustering and SNR score to rank each gene in every cluster. ▪ The top scored genes from each cluster are gathered and a new feature subset is generated. In the second stage, the new feature subset is used as input to the PSO and optimized feature subset is produced. ▪ Support vector machine (SVM), k-nearest neighbor (k-NN) and Probabilistic Neural Network (PNN) are used as evaluators ▪ Leave one out cross validation approach is used for validation. |
| PSO-Decision theoretic Rough set [50] |  |
– | ▪ The author proposes a new PSO based wrapper, single objective FS approach by developing new initialization and updating mechanisms. |
| Redundant Gene selection using PSO(RGS-PSO) [123] | – |  |
▪ Redundant gene selection using PSO (RGS-PSO) is a novel approach. ▪ Where the fitness function of PSO explicitly measures feature relevance and feature redundancy simultaneously. |
| ACO-BPNN [54, 56] | – |  |
▪ The ant colony optimization (ACO) algorithm is introduced to select genes relevant to cancers. ▪ The multi-layer perceptrons (MLP) and support vector machine (SVM) classifiers are used for cancer classification. |
| BBO-RF,BBO-SVM [114] |  |
– | ▪ Two-hybrid techniques, Biogeography – based Optimization – Random Forests (BBO – RF) and BBO – SVM (Support Vector Machines) with gene ranking as a heuristic, for microarray gene expression analysis is proposed. ▪ The BBO algorithm generates a population of candidate subset of genes, as part of an ecosystem of habitats, and employs the migration and mutation processes across multiple generations of the population to improve the classification accuracy. ▪ The fitness of each gene subset is assessed by the classifiers – SVM and Random Forests |
| Wrapper using KNN [60, 61], Wrapper using 1-NN [62] | – |  |
▪ Using the Naïve Bayes learner, the authors perform wrapper feature selection followed by classification, using four classifiers (Naïve Bayes, Multilayer Perceptron, 5-Nearest Neighbor, and Support Vector Machines). ▪ The above results are compared to the classification performance without feature selection. |
| Bat Algorithm –Rough set method [124-127] |  |
– | ▪ A fitness function based on rough-sets is designed as a target for the optimization. ▪ The used fitness function incorporates both the classification accuracy and a number of selected features and hence balances the classification performance and reduced size. |
| Improved Ant Colony Optimization-SVM [53-55, 128] |  |
– | ▪ A nature inspired and novel FS algorithm based on standard Ant Colony Optimization (ACO), called improved ACO (IACO), was used to reduce the number of features by removing irrelevant and redundant data. ▪ The selected features were fed to support vector machine (SVM), a powerful mathematical tool for data classification, regression, function estimation and modeling processes, in order to classify major depressive disorder (MDD) and Bipolar disorder (BD) subjects. |
| Constructive approach for Feature Selection(CAFS) [128] | – |  |
▪ The vital aspect of this wrapper algorithm is the automatic determination of NN architectures during the FS process. ▪ It uses a constructive approach involving correlation information in selecting features and determining NN architectures. |
| Wrapper ANFIS-ICA method [57] |  |
– | ▪ The paper presents a novel forecasting model for stock markets based on the wrapper ANFIS (Adaptive Neural Fuzzy Inference System)-ICA (Imperialist Competitive Algorithm) and technical analysis of Japanese Candlestick. ▪ Two approaches of Raw-based and Signal-based are devised to extract the model's input variables with 15 and 24 features, respectively. ▪ In this model, the ANFIS prediction results are used as a cost function of wrapper model and ICA is used to select the most appropriate features. |
4. FEATURE SELECTION METHODS FOR MICROARRAY DATA
Microarrays are high dimensional data [78], which represent a matrix, where the row of the matrix represents the number of genes and columns represent a number of samples. Microarrays are used to measure the expression level of thousands of gene simultaneously. The major issue in Microarray data analysis is the curse of Dimensionality. In the literature, microarray data is widely used for cancer classification. Due to the curse of Dimensionality problem, it may lead to overfitting of the classifier. This issue can be resolved by dimensionality reduction in microarray data. For a few number of genes say 5, the performance of the classifier is poor, but gradual increase in the number of selected features up to a point improves the performance. However, when more features are included beyond the threshold, the performance gets worse. If all features are included then performance deteriorates markedly. This means that including too many irrelevant features can actually worsen the performance of a learning algorithm, and hence shows the need for feature selection or feature extraction in microarray data for supervised learning. Feature extraction involves various techniques such as PCA, various clustering technique such as c-means clustering, hierarchical clustering, etc.
The major objectives of feature selection technique in microarray data are
- To remove noisy and irrelevant genes from the current data set.
- Improve the computational cost.
- Avoid overfitting of the classifier.
In the current paper, we have classified the feature selection techniques for microarray data as nonsoft computing based and soft computing based feature selection. From the above-mentioned feature selection methods, all statistical methods (filter methods), as well as sequential wrappers and some of the embedded methods, belong to the nation soft computing feature selection category, and most of the hybrid methods of feature selection come under soft computing based feature selection category.
In literature Univariate, filter methods have been extensively used in microarray data to identify biomarkers, which is a parametric technique. Beside parametric techniques, non-parametric techniques can also be applied for feature selection. In microarray data, feature selection becomes a critical aspect when tens of thousands of features are considered. The wrapper approach takes the attention as the filter method for feature selection in case of microarray data due to its high computational cost. It is due to the fact that, as the number of features grows, the space of feature subset grows exponentially. Furthermore, they have the risk of overfitting due to the small sample size of microarray data. Therefore, the wrapper approach has been listed and considered in the literature for feature selection. Hybrid and ensemble methods are widely used in the literature for microarray data analysis as it overcomes the limitations of both filter and wrapper approach. Table 8 shows the different feature selection techniques used for Microarray data
| Name of the Method | Filter | Wrapper | Embedded | Other |
|---|---|---|---|---|
| Signal-to-noise-Ratio(SNR) [65-69] | Y | X | X | X |
| t-test [121] | Y | X | X | X |
| Euclidean Distance [66, 67] | Y | X | X | X |
| Bayesian Network [64] | Y | X | X | X |
| Information Gain (IG) [63] | Y | X | X | X |
| Correlation-based Feature Selection [70] | Y | X | X | X |
| FCBF [71] | Y | X | X | X |
| ReliefF [69] | Y | X | X | X |
| mRMR method [72] | Y | X | X | X |
| EFA [73] | Y | X | X | X |
| PCC [66, 86] | Y | X | X | X |
| SAM [87, 115] | Y | X | X | X |
| correlation coefficient [114] | Y | X | X | X |
| redundancy based filter [110] | Y | X | X | X |
| BIRS [74] | X | Y | X | X |
| Classical wrapper search algorithm [75] | X | Y | X | X |
| GA-KDE-Bayes [76] | X | Y | X | X |
| SPS [77] | X | Y | X | X |
| RGS-PSO [118] | X | Y | X | X |
| FRFS [79] | X | X | Y | X |
| IFP [80] | X | X | Y | X |
| KP-SVM [81] | X | X | Y | X |
| PAC-Bayes [82] | X | X | Y | X |
| Random Forest [83] | X | X | Y | X |
| Recursive Feature Elimination (SVM-RFE) |
X | X | Y | X |
| Ensemble feature selection (EF) [84] | X | X | X | Y |
| MFMW [85] | X | X | X | Y |
| SNR-PSO [49] | X | X | X | Y |
| BBO [117] | X | X | X | Y |
4.1. Nonsoft Computing Method Performance Analysis for Microarray Data
This section reviews some of the non-soft computing based feature selection methods used in microarray data listed in Table 8. Selection methods involving evaluation of individual features, sequential forward selection, sequential backward selection and many more statistical approach are included in this category (Table 9).
| Name of the Method | Key Idea | Performance Analysis |
|---|---|---|
| Euclidian distance and Pearson correlation feature selection [66] | • Euclidian distance and Pearson correlation coefficient for feature selection • SVM classifier with different kernel |
Distance-based method outperforms for SVM with a linear kernel. |
| SNR [65], t-test [121] | • k-means for attribute clustering • Signal to noise ratio and t-statistics for feature selection • SVM, kNN, PNN, FNN are used for classification. . |
The performance of SVM classifier gives a better result for the 5 features using k-means-SNR and k-means-t-test approach. |
| Filter approach [63] | • IG, RA, TA, and PCA for feature selection. • SVM, kNN, DT, NB, and NN for classification. |
The best classification accuracy is achieved by using a subset of 250 features chosen by IG based method for SVM classifier. |
| mRMR [72] | • mRMR for feature selection • NB, SVM, LDA for classification |
The computational cost of mRMR is low and the classification accuracy is high in comparison to maximum dependency and maximum relevance for all datasets. |
| Best Incremental Ranks Subset(BIRS) [74] | • BIRS (wrapper), nonlinear correlation measure based entropy and IG feature selection methods. • NB,IB,C4 for classification |
The computational complexity of BIRS is better in comparison to CFS, FCBF. |
| Kernel panelized SVM(KP-SVM) [80] | • KP-SVM for feature selection • SVM for classification |
The advantage of KP-SVM in terms of computational effort is that it automatically obtains an optimal feature subset, avoiding a validation step to determine how many ranked features will be used for classification. |
4.2. Soft Computing Methods performance Analysis for Microarray Data
Feature subset selection in the context of many practical problems such as diagnosis of cancer-based on microarray data presents an instance of a multi-criteria optimization problem. The multi-criteria to be optimized include the accuracy of the classifier, cost, and risk associated with the classification which in turn depends on the selection of attributes used to describe the patterns. Evolutionary algorithms offer a significant approach to multi-criteria optimization (Table 10).
| Name of the Method | Key Idea | Performance Analysis |
|---|---|---|
| A hybrid approach with GA wrapper [48] | ▪ Ensemble feature selection using entropy-based feature ranking, t-statistics, and SVM-REF ▪ GA is applied to search an optimal or near optimal feature subset from the feature pool. ▪ SVM for classification |
SVM-RFE shows better classification performance than other selection techniques for all datasets. |
| Redundant gene selection using PSO [122] | ▪ Gene selection by RGS-PSO ▪ SVM,LG,C45,kNN,NB are used for classification |
RGS-PSO and mRMR with 20genes are the best two methods, which have the top averaged BACC scores 0.818. |
| Rough set and SVM based [123] | ▪ Rough set and MRMS for gene selection ▪ SVM for classification |
The MRMS selects a set of miRNAs having a lowest B.632+ bootstrap error rate of the SVM classifier for all the data sets. The better performance of the MRMS algorithm is achieved due to the use of rough sets. |
| ACO [52] | ▪ ACO for feature selection ▪ In this paper, each gene is viewed as a node on the TSP problem. The nodes on the tour generated by the ant colony are the selected genes for cancer classification. ▪ BPNN for classification . |
ACO feature selection algorithm improves the performance of BPNN. Area under ROC curve (AUC) value after feature selection increased from 0.8531 to 0.911. |
| Rough set based [128] | ▪ Rough set theory for feature selection by maximizing the relevance and significance of selected genes. ▪ K-NN and SVM for classification |
The performance of proposed MRMS criterion is better than that of Max-Dependency and Max-Relevance criteria in most of the cases. Out of total 28 cases, the MRMS criterion achieves significantly better results than Max-Dependency or Max-Relevance in 25 cases. |
From the study, the recent trend of feature selection has been shifted to hybrid and ensemble method from the classical feature selection method like a filter, wrapper and embedded. For microarray data, the hybrid and ensemble method of feature selections are extensively used. In the current review, we have categorized the classical feature selection techniques and other technique like hybrid and ensemble approach in soft computing and non soft computing technique of feature selection. From the study, it is apparent that researchers are more focused towards the soft computing approach of feature selection rather than non soft computing approaches for high dimensional data like microarray data. Because in supervised learning, the model efficiency is highly dependent on training, the model is trained with significant features to enhance the efficiency of the model. The soft computing feature selection techniques mostly use evolutionary algorithms for feature selection to get the optimal and discriminative features. Moreover, the soft computing technique with hybrid approach is more desirable to reduce the computational cost and overfitting of the model.
5. DISCUSSION AND FUTURE RESEARCH DIRECTION
Various methods of feature selection for microarray data are discussed in this paper. From the literature survey, non-soft computing approaches like the statistical approach of feature selection give accuracy to the classifier without considering the correlation of features, whereas soft computing based feature selection adopts different search strategy to select optimal feature subsets in association with non-soft computing based feature selection such as filter and wrapper methods. From the literature, it is observed that hybrid soft computing approaches of feature selection are used widely for different applications in comparison to non hybrid techniques. For high dimensional data like microarray data, the non hybrid non soft computing approaches (like filter technique) were used previously for most of the microarray dataset. But now a days, hybrid soft computing techniques of feature selection are mostly preferred to get the optimal feature subset over non hybrid non soft computing techniques of feature selection due to flexibility and efficiency in selecting features from high dimensional data. There can be future research to develop algorithms using sequential and random search strategies for clustering and classification tasks respectively. The research can be extended to identify the biological relevance of feature subsets after applying non-soft computing as well as soft computing technology instead of only considering the model performance. The performance needs to be evaluated not only based on classification accuracy but also evaluating the metrics like sensitivity and specificity.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.