Identification of Better Gene Expression Data for Mosquito Species Classification Using Radial Basis Function Network Methodology
Abstract
Background:
Investigation in bioinformatics has developed promptly in latest years owing to improvements in sequence excavating techniques. Gene sequences in DNA are supplemented with great extent of information, but the intricacy and complexity of this information causes difficulty in analyzing it by using standard classical methods of classification. In this work, a Radial Basis Function Network (RBFN) methodology with self-network arrangement is presented for identification of mosquito species based on the genetic design content of ITS2 ribosomal DNA sequences.
Methods:
A number of data sequences in varying sizes of different vectors corresponding to Anopheline, Aedes and Culex genera are used to develop genera specific as well as comprehensive RBFN species identifiers. The recall and generalization ability of the proposed species identifiers are analyzed and further validated through bootstrap validation method. The genera specific RBFN identifiers are found to provide accurate identification of mosquito species of individual genera. However, the comprehensive RBFN model is found to exhibit better species identification ability and can be advantageously used for species identification of more mosquito genera.
Results & Conclusion:
The results demonstrate the usefulness of the RBFN methodology for accurate identification of mosquito species depending on the nucleotide data of ITS2 ribosomal DNA sequences.
1. INTRODUCTION
Exploration of bioinformatics has developed hastily in recent years due to the advances in molecular biology techniques. One of the most vital research interests in computational biology is sequence mining. It is more difficult to extract knowledge hidden in the sequences than to generate biological sequences. Models and data analysis has become a crucial aspect of biological sequence mining. Several tasks related to sequence mining such as pattern discovery, classification, prediction and clustering can be carried out by statistical, neural network or data mining models [1-5]. Such techniques can be used to capture the knowledge or patterns in order to predict, classify or analyze the sequence data. However, the phenomenal growth of sequence data has made the database search computationally intensive and even more forbidding. Gene sequences in DNA are augmented with huge amount of information, but the intricacy and complexity of this information makes difficult in analyzing it by using standard classical methods a challenging task.
Genetic level analysis for identification of the species in mosquito is very crucial as the species act as a vector for several diseases such as malaria, filarial, Japanese encephalitis and dengue. Among these diseases, burden of malaria is fairly high and results in heavy toll of life. Anopheles mosquito species act as a vector for malaria which is widely spread throughout the globe [6-8]. Among 3,500 species of mosquitoes, nearly 430 are Anopheles in which around 30-40 species act as a vector for malaria. Aedes is a genus of mosquito originated in tropical and subtropical zones, but it has spread through human activity to all continents with the exception of Antarctica [9]. The genus of Aedes contains over 700 species. Many of the Aedes species transmit potentially serious human diseases. Culex is a genus of mosquito in which several species serve as vectors of diseases. The genus of Culex has widespread geographical distribution [10] and consists of about 767 species. Classical methods of distinguishing species through genetic analyses have reduced dependence on error-prone morphological and anatomical bases of classification [11]. In the taxonomic classification it is quite difficult to distinguish the sibling species that bear similar morphological and anatomical features but differ at the genetic level. Therefore, for quick identification of a mosquito vector, it is always possible to target a conserved sequence at the genetic level, which is pretty species specific and shows substantial difference even among the sibling species. Internal Transcribed Spacer (ITS) region is widely used in taxonomy and molecular phylogenetics [12, 13]. The ITS2 region located between the 5.8S and 28S gene is highly conserved and species specific. This region is commonly used for DNA sequencing in mosquito genera of Anopheles, Culex, and Aedes [14]. The ITS2 region has been proven useful for differentiating between closely related species of mosquitoes [15-17]. This region has also been extensively targeted for species classification, phylogenetic and RNA structure-related analysis [18, 19].
More precise and efficient computational tools are needed to extract genetic level information in the gene sequences and to distinguish mosquito species with minimum or no misclassification. Artificial Neural Networks (ANNs), as one of the Artificial Intelligence (AI) methods, play important role in scientific investigations. ANNs have been used as prediction and classification tools for several applications in the field of bioinformatics including protein structure prediction [20, 21], DNA sequence analysis and biological pattern recognition [22-24], RNA structure related analysis [13, 16, 19] and prediction of bacterial promoter sequences [25-27]. Recently, ANNs are also used for species identification in mosquitoes [28-30]. The wide use of ANNs for prediction and identification is due to their ease of training and flexibility to process high amounts of information with good generalization ability. Although, ANN are widely used for classification and identification problems, most of the ANN models aim at finding the network parameters using a fixed network configuration. It may not be possible to train the ANN to reach a desired level of performance if the network does not have enough computational units, or if the learning algorithm fails to find the optimal network parameters. Therefore, automatic configuration of the network while establishing optimal network parameters is extremely useful in classification and identification of problems. In this work, a Radial Basis Function Network (RBFN) methodology with automatic network configuration is presented for the identification of mosquito species based on the genetic pattern information content of ITS2 ribosomal DNA sequences. A number of data sequences in varying sizes of different vectors corresponding to Anopheline, Aedes and Culex are used to develop genera specific RBFN species identifiers. Further, a comprehensive RBFN species identifier is also presented for mosquito species identification of more genera. The recall and generalization ability of the RBFN species identifiers are analyzed and further validated through bootstrap validation method.
2. DATA SELECTION AND ITS SIGNIFICANCE
Precise identification of the target species of mosquito has direct medical and practical implications, particularly in developing vector control strategies. Among the vector species of mosquito born diseases, the species belonging to the genera of Anopheles, Aedes and Culex are reported to be involved in the transmission of a variety of vector-borne diseases. Prioritizing the need for detecting the species that act as vectors for several diseases, the present work is targeted on the identification of species of mosquitoes of these three genera.
2.1. Data Collection
The ribosomal DNA sequence (ITS2) data of 15 species of Anopheles genera, 10 species each of Culex and Aedes genera collected in fasta format from National Center for Biotechnological Information (NCBI) nucleotide data base (www.ncbi.nlm.nih.gov/), is used for the computational experiment. Each sequence collected from NCBI nucleotide data base has a specific accession number. For example, the ITS2 part of representative sample sequence of Anopheles saporoi belonging to the Anopheles genera has the NCBI accession number AY425338.1. Similarly, the sample sequence of Aedes albiradius belonging to the Aedes genera has the NCBI accession number FM211137.1 and the Culex pipens belonging to the Culex genera has the NCBI accession number AM084683.1. The length of the sequences varies in the range of 200 to 500.
2.2. Data Significance
Correct vector identification is imperative to design strategies for managing vector-borne diseases. Since many closely related species of mosquitoes are nearly indistinguishable morphologically, it is difficult to identify mosquitoes especially sibling species correctly. As a consequence, DNA-based approaches have gained increasing importance in mosquitoes identification. The ITS2 ribosomal DNA sequences have proven to be useful for differentiating the closely related species of mosquitoes. The ITS2 region, located between the 5.8S and 28S gene is found to be highly conserved and species specific, and the gene sequence data of this region deposited in NCBI data bank is considered for classification and analysis of the mosquito species. Though the identification of the species listed in NCBI data is based on different criteria, the NCBI assigns a unique identifier to each species and the ITS2 region of the rDNA sequences corresponding to the unique identifier is used to define the species.
3. RBFN SPECIES IDENTIFICATION METHODOLOGY
In mosquitoes, because of the interspecific variability and intraspecific homogeneity in spacer sequences, the species cannot be easily distinguished by just looking at the sequence information. The development of an efficient species classifier is required to identify the closely related species of mosquitoes. Thus, an RBFN classifier with its automatic configuration is developed for the identification of mosquito species based on the gene sequence information contained in the conserved structure of the transcribed spacer, ITS2 region. The RBFN classifier presented in this work is used to distinguish and identify the species of Anopheles, Aedes and Culex genera. Radial Basis Function Network (RBFN) has been considered as viable tool for applications in systems modeling and state estimation [31-35]. The RBFN architecture is simple and consists of one input layer, one hidden layer and one output layer, the structure of which is shown in Fig. (1). The RBFN algorithm along with its automatic configuration is given in Appendix A.
3.1. Configuring RBFN for Species Identification
In this work, RBFN is configured for mosquito species identification using the data of ITS2 ribosomal DNA sequences corresponding to different mosquito vectors. The automatic configuration of the network is carried out by using a Hierarchically Self-Organizing Learning (HSOL) algorithm. The RBFN used for mosquito species identification has a three layered architecture with input, hidden and output layers, each layer comprising its own nodes, as shown in Fig. (2). All nodes in the input layer are connected to the hidden layer nodes, and connections exist between the hidden and output layer nodes. The input layer represents the sequence data, the hidden layer processes the nonlinear information, and the output layer depicts sequence classes. The nodes in the input layer do not perform any numerical processing; all numerical processing is done by the hidden and output layer nodes. The number of nodes in the input layer is dictated by the chosen sequence encoding schema and the number of the output layer nodes is determined by the species classes representing the network. The nodes in the hidden layer are automatically configured by the HSOL algorithm. The other network parameters that are involved in configuring the RBFN are: the learning rate η, error margin εm, initial nominal variance σo, initial effective radius ro, lower bound on radius rl, radius decrement rate rd, decay factor for error gradient α, and increment rate for saturation criterion β.
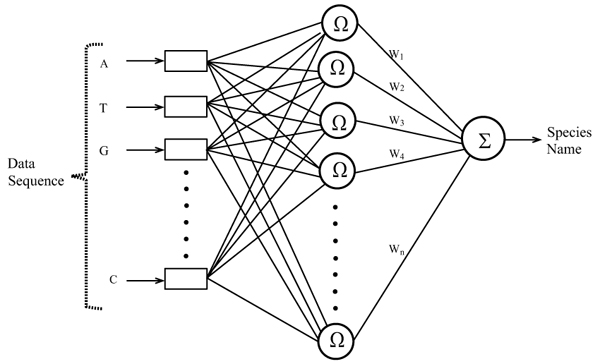
3.2. Encoding of Species Data to RBFN
Data encoding plays a crucial role in configuring the RBFN model for species identification. The encoding method can have a significant effect on the learning ability and accuracy of the gene classification system. The data encoding should be in an acceptable format such that the trained network can make clear distinction between the different classes of species data. ITS2 ribosomal DNA sequences of mosquito species are made up of four bases, Adenine-A, Thyamine-T, Guanine-G and Cytosine-C. These bases are denoted by a numerical vector which forms the input to the network. The numerical values to encode the input data sequences and to denote the output species are selected so as to yield effective training and classification performance of the network. The bases of ribosomal DNA sequences A, T, G and C representing the inputs to the network are coded with binary values by assigning with A = {0 0}, T = {0 1}, G = {1 0}, C = {1 1}. This input assignment requires the number of nodes in the input layer of the network to be twice the length of the sequence. The output coding that represents the species names is expressed in real coding. The input and output coding assigned for each of the species net is shown in Table 1. This coding is chosen after testing the network using various input and output coding combinations.
3.3. Genera Specific RBFN Species Identifiers
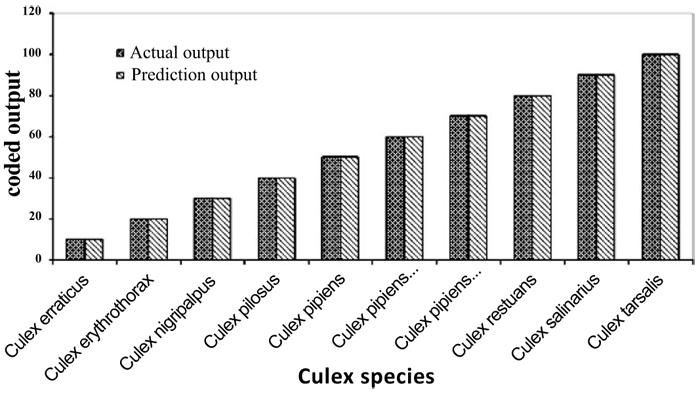
The RBFN species identifiers are configured for each of the Anopheles, Aedes and Culex genera. The data of total 15 species of Anopheles genera, 10 species each Aedes and Culex genera is used for configuring the network. Each species is considered with 4 sequences in which three sequences are used for training and one sequence is used for testing. Thus, Anopheles network involves 45 sequences for training and 15 sequences for testing. Each Aedes and Culex network involves 30 sequences for training and 10 sequences for testing. The bases A, C, T, and G of ribosomal DNA sequences representing the network inputs are coded with binary values and the species names specifying the network output are coded with real numbers. The network structure shown in Fig. (2) is employed to treat the data given in Table 1. The normalized data of outputs is used to train the networks along with the corresponding input data. The network interconnection weights are initialized by assigning random numbers in the range of - 0.2 to 0.2. Each genera net training involves the sequential treatment of the data sets of the input sequences to map with the output coding specified for the species. The species corresponding to each of the genera are randomly selected for training, and the species that are not involved in training are randomly employed for testing.
The network should accommodate the rDNA data sequences of varying lengths in its training and prediction. For this, the network input nodes are to be chosen so as to suit the sequence of any species irrespective of its size. After studying different options, a simple format is employed to manage the network with the input data sequences of different sizes. According to this format, the number of input nodes to the network is specified in terms of binary coding for the sequence that is larger in size. This format facilitates the network to accommodate the sequences of varying sizes by appropriately filling the empty nodes with the binary codes of the last four bases of the respective sequence. This approach of training and prediction to treat the data of rDNA sequences of different sizes has been proven useful in earlier studies [29, 30].
| S. No | Genera Name | Species Name | Input Coding | Output Coding |
|---|---|---|---|---|
| 1 2 3 5 6 7 8 9 10 11 12 13 14 15 |
Anopheles |
aconitus annulipes bancroftii farauti fluviatilis lesteri maculipennis messeae nuneztovari oswaldoi pullus saperoi sinensis stephensi subpictus |
A = {0 0}, T = {0 1}, G = {1 0}, C = {1 1}. |
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 |
| 1 2 3 4 5 6 7 8 9 10 |
Aedes |
albiradius ashworthi australis circumluteolus cretinus fontenillei nigropterum palpalae punctor simpsoni |
A = {0 0}, T = {0 1}, G = {1 0}, C = {1, 1}. |
10 20 30 40 50 60 70 80 90 100 |
| 1 2 3 4 5 6 7 8 9 10 |
Culex |
erraticus nigripalpus pilosus pipiens pallens pipiens salinarius territans tigripes torrentium tritaeniorhynchus |
A = {0 0}, T = {0 1}, G = {1 0}, C = {1 1}. |
10 20 30 40 50 60 70 80 90 100 |
In RBFN model building, the HSOL algorithm enables to provide comprehensive learning with automatic recruitment of RBFs while optimizing the network parameters. Input and output mapping comparison of target and actual values continue until all the data sequences of the training species are learned within an acceptable over all error. During the classification and generalization phase, the trained RBFN itself operates in a feed forward manner.
3.4. Comprehensive RBFN Species Identifier
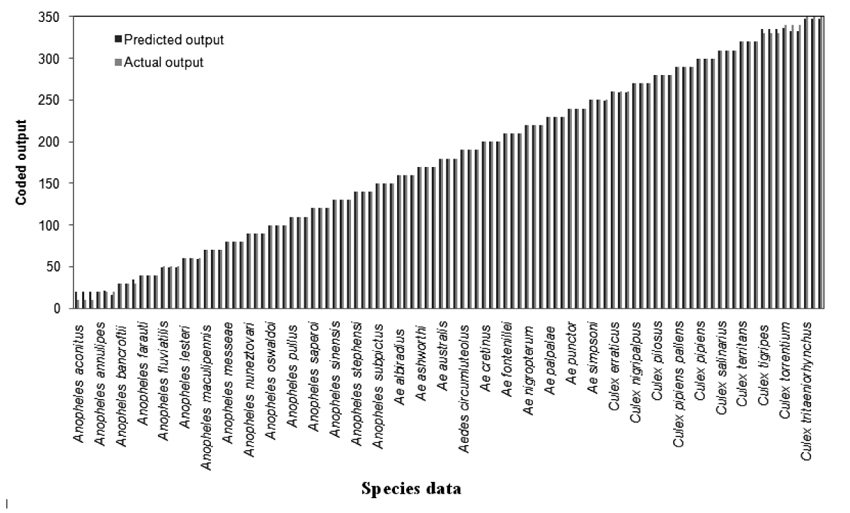
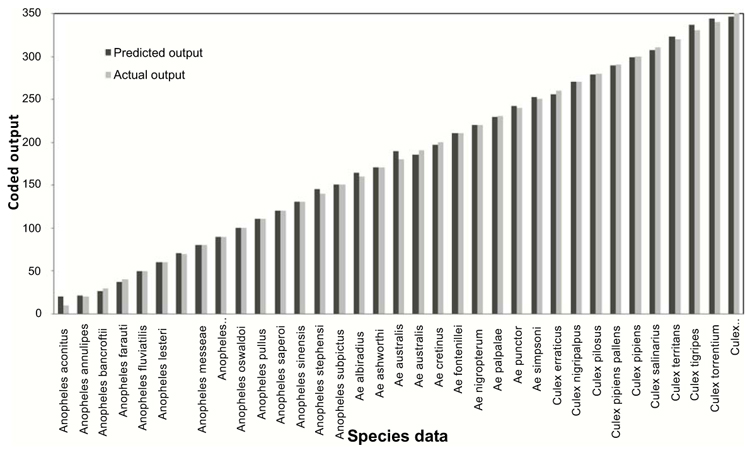
The comprehensive species identifier is a multi-input and single-output RBFN, in which all the data sequences corresponding to the species of the three genera are treated as inputs to the network along with their corresponding species names as the network outputs. As in individual RBFN, the bases A, T, G, C of ribosomal DNA sequences in binary coding form the network inputs, and their corresponding species names in real coding denote the network outputs. The structure of combined RBFN is similar to that in Fig. (2), where the data sequences corresponding species of all the three genera, along with the corresponding output representation given in Table 2, are sequentially and iteratively used to train the network. The data of 105 random sequences from the 35 species of the three genera are used for training and the untrained data sets of 35 sequences corresponding the species of all the three genera, are used to evaluate the network predictive performance. The number of input nodes used to accommodate the sequences of varying lengths in comprehensive RBFN is the same as in individual RBFN. The network training is performed using HSOL algorithm. The initialization of the network parameters in combined model is the same as in individual model. All the data sets corresponding to input sequences with their binary coding, and the output species with their numerical coding are sequentially used to train the network model. The network parameters are optimized to establish the relationships between input and output data. A quadratic error function, based on the actual and predicted outputs, forms the objective function, which is minimized through iterative convergence.
| S.No. | Genera name | Species name | Input coding | Output coding |
|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
Aedes Anopheles Culex |
albiradius albopictus ashworthi australis belleci cinereus circumluteolus cretinus fontenillei geminus albitarsis Annuples arabiensis atroparves culifacies maculipennis melanoon nuneztvan puulus sachrov saporoi sinensis sundacius superpictus erraticus erythrothorax nigripalpus pilosus pipiens pipienspallens pipiensquinquefasciatus restuans salinarius tarsalis |
A = {0 0} T = {0 1} G = {1 0} C = {1 1} A = {0 0} T = {0 1} G = {1 0} C = {1 1} A = {0 0} T = {0 1} G = {1 0} C = {1 1} |
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330 340 |
4. RESULTS AND DISCUSSION
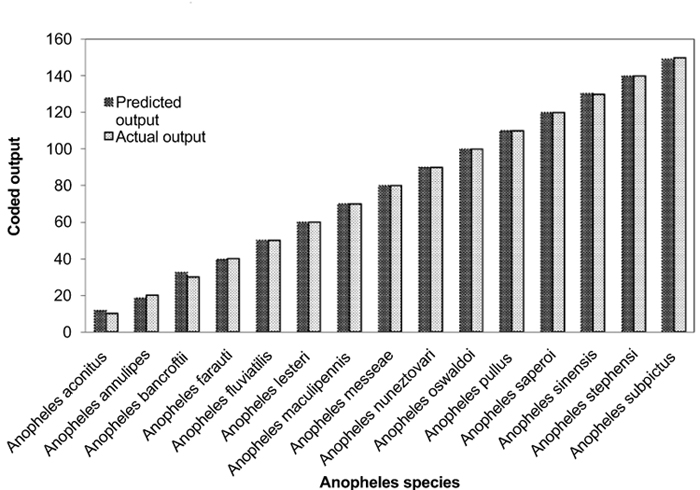
Individual RBFN models are developed for anopheles, aedes and culex genera using the input and output data corresponding to the species of these genera. The presentation of data to RBFN is briefed in the earlier section. The RBFN parameters are set as: learning rate (η) = 0.00025, error margin (εm) = 0.001, initial nominal variance (σo) = 0.0021, initial effective radius (ro) = 5.0, lower bound on radius (rl )= 0, radius decrement rate (rd) = 0.995, decay factor for error gradient (α) = 1.0 x 10-09, and increment rate for saturation criterion (β) = 1.0 x 10-05. For network training, all the data sets representing the species inputs and outputs are sequentially employed in each iteration and iterations are performed until the network is optimally configured via HSOL algorithm. The number of iterations required for convergence, number of RBFs generated, training error evaluated and training time required for each of the networks are given in Table 3. The trained and learned RBFNs are then subjected to assess their recall and generalization abilities. In the recall phase, the prediction ability of the trained networks is evaluated by using the same input sequences as used for training. Each of these RBFNs has shown almost 100% recall ability. The generalization performance of the networks is evaluated by using the species sequences that are not involved in training. This is referred here as conventional cross validation. Thus, 15 data sequences corresponding to the species of anopheles genera, 10 data sequences corresponding to the species of each aedes and culex genera, are used to test the generalization ability of the individual RBFN models. The comparison of the model predictions with the actual output species representations in Figs. (3-5) shows the effective generalization performance of the individual RBFN species identifiers. The generalization ability of the RBFN models is further assessed in terms of Mean Squared Error (MSE) and correlation coefficient (R2) defined in Appendix B. These results in Table 4 further demonstrate the efficiency of the RBFN methodology for accurate identification of mosquito species based on the nucleotide data of ITS2 ribosomal DNA sequences.
| Modeling Configuration | No. of Iterations | No. of RBFNs Generated | Minimum Training Error | Training Time (Seconds) |
|---|---|---|---|---|
| Anapheles Net Aedes Net Culex Net Combined Net |
50 50 50 100 |
28 26 19 29 |
0.0013 0.0001 0.0041 0.0015 |
10 10 10 30 |
| Species Identifier | Conventional Cross Validation |
Bootstrapping Cross Validation |
||
|---|---|---|---|---|
| MSE | R2 | MSE | R2 | |
| Anapheles net | 0.000196 | 0.98991 | 0.00323 | 0.9723 |
| Aedes net | 0.000187 | 0.99437 | 0.00043 | 0.9834 |
| Culex net | 0.000183 | 0.99745 | 0.00421 | 0.9856 |
| Comprehensive net | 0.000283 | 0.98330 | 0.00134 | 0.9753 |
A comprehensive RBFN model is also developed for species identification of anopheles, aedes and culex genera using the input sequence data in binary coding and output species representation in real coding as given in Table 2. The combined RBFN structure is similar to that of genera specific RBFN structure in Fig. (2) with multiple input nodes and single output node. The parameters specified for this RBFN structure are same as in genera specific model structure. The data representation as well as training of this comprehensive network is briefed in the earlier section. In contrast to the genera specific RBFN, this comprehensive RBFN model involves sequential treatment of all the input data sequences representing the species of the three genera along with their respective species output coding. Thus, the data sets in Table 2 are sequentially employed and iterated until the network is optimally configured by HSOL algorithm. The number of iterations required for convergence, number of RBFs generated, training error obtained and training time required for this comprehensive network are given in Table 3. The entire code was written and executed using C language. The computer configuration used is Intel(R) Core ™ i7-4702MQ CPU @ 2.20GHz 2.20 GHz and the system type is 64-bit Operating System, x64-based processor.
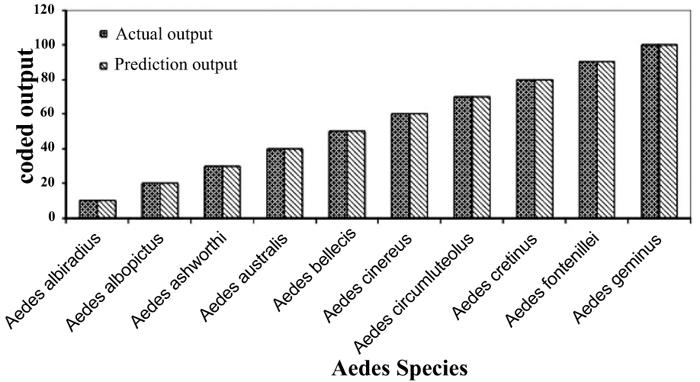
The trained and learned comprehensive RBFN is further studied through conventional cross validation to assess its recall and generalization ability. The comparison of this combined network model predictions with the actual species representations for the recall and generalization phases are shown in Figs. (6 and 7). The generalization performance of the combined network is further evaluated in terms of MSE and R2 as given in last line of Table 4. These results exhibit better performance of the comprehensive model for species identification of mosquito genera.
Model validation is an important step in ascertaining the reliability of models before they can be used in decision making. The predictive performances of trained and learned RBFNs are further assessed by using bootstrapping procedure. This procedure enables to validate the full n-subject model. The RBFN parameters of individual and combined models for this approach are kept same as in earlier model configurations. According to this bootstrap, the Anopheles genera net is validated by performing 9 rounds of bootstrapping with the use of all 45 gene sequences. In each round, 40 data sequences corresponding to the species of Anopheles genera are randomly assigned for training while the remaining 5 data sequences are assigned for validation. Thus, the model in each round is assessed through training and validation. The same boot strapping procedure is employed to assess the performance of other genera specific RBFN models and the comprehensive RBFN model. The number of iterations required for convergence, number of RBFs generated, training error obtained and training time required for the genera specific networks and comprehensive network of this bootstrap procedure are found to be nearly same to that of trained and learned RBFN models used in recall and generalization phases. The model validation results of MSE and R2 evaluated through the bootstrap approach to assess the predictive accuracy of the fitted models are shown in Table 4. These results confirm the predictive accuracy of the RBFN models developed in this study.
Recent studies have shown the effectiveness of intelligent computational tools such as Artificial Neural Networks (ANN) for rapid and reliable identification of mosquito species. The genetic data base of mosquitoes has been exploited by such methods to differentiate even closely related species of mosquitoes. Banerjee et al (2008) [29] presented a multilayered feed-forward neural network model structure for classification and identification of mosquito species based on the Internal Transcribed Spacer 2 (ITS2) data of ribosomal DNA string. Two network models, namely, a Multi-Input Single-Output Neural Network (MISONN) and Multi-Input Multi-Output Neural Network (MIMONN) have been configured in which the MISONN was found to provide effective performance in distinguishing and identification of mosquito species. However, the above reported work was confined to the analysis of species of single mosquito genera only based on the data of 18 species of Anopheles mosquito vectors. The above neural network modeling approach has been further extended by Venkateswarlu et al. (2012) [30] for classification and identification of species of more mosquito genera by presenting a Hierarchical Artificial Neural System (HANS) in two levels, in which the first level has a single network that serves as a genera classifier and the second level has multiple networks that perform as species identifiers. Ribosomal DNA sequence data of 34 species of Anopheles, Aedes, and Culex genera, each species with 6 sequences were used for training and validation. The method of HANS was found to provide accurate genera classification and rapid species identification. However, the genera net and species nets involved in HANS were found to require more training efforts. Very recently, Lorenz et al. (2015) [36] employed ANN for identification and classification of mosquitoes based on the wing shape characters of the species. A data base of 32 principal components representing the wing shape characteristics of 17 mosquito species of Anopheles, Aedes and Culex genera were analyzed by using a multi layer perception ANN classifier. Species identification by this method was found to be accurate enough. Although the ANN technique of Lorenzo et al. can handle large amount of data, unique variations in wing shape data is required for correct analysis of mosquitoes. Though the above reported ANN configurations are found effective for classification and identification of mosquito species, their major limitation is the heuristic configuration of the network parameters and computational units which may restrict them in achieving the desired performance. The RBFN methodology of this work overcomes such a limitation by automatically configuring the network with optimal selection of computational units.
This work differs from the earlier reported works with respect species involved for analysis as well as the method of species identification. The analysis of the results exhibits accurate identification of mosquito species by genera specific RBFN models, but their application is limited to the identification of species of individual genera. Even though, the genera specific RBFN species identifiers of this work provides marginally improved performance over the Multi-Input Single-Output Neural Networks (MISONN) of earlier reported works, the major advantage comes from the comprehensive RBFN of this work. The training effort as well as the training time required for this comprehensive RBFN with automatic learning, is found to be much lower to the above reported neural network configurations. This method is found to exhibit better species identification ability and it can be advantageously extended for identification of species of more mosquito genera.
This is the first study for proposing and using such an automatically configured RBFN for classification and identification of mosquito species based on ITS2 ribosomal DNA sequence data. Though the comprehensive RBFN model of this study is quite useful for accurate identification of mosquito species of different genera, the computational effort required for automatic configuration of RBFs and interconnection weights increases with the increase of number of genera and species. The methodology can be applied with similar success to identify the other species of Anopheles, Aedes and Culex genera as well as the species of other geographical varieties, if the network is trained properly by involving analogous species of such genera.
CONCLUSION
Rapid and accurate identification of mosquito species are of paramount importance for taking control measures against deadly diseases like malaria, filariasis, encephalitis, dengue and so on. Genetic identification is the conformation for any kind of biological classification. The data sequences of ITS2 region considered for mosquito species identification in this work are widely used to extract the phylogenetic relation due to their well-conserved nature in a particular species. In this work, a Radial Basis Function Network (RBFN) methodology with automatic network configuration is presented for identification of mosquito species based on the genetic pattern information content of ITS2 ribosomal DNA sequences. A number of data sequences in varying sizes of different vectors corresponding to Anopheline, Aedes and Culex are used to develop genera specific RBFN species identifiers and a comprehensive RBFN species identifier. The recall and generalization ability of the RBFN species identifiers are analyzed and further validated through bootstrap validation method. The genera specific RBFN models are found to provide accurate identification of mosquito species of individual genera. The comprehensive RBFN species identifier is found to exhibit better species identification ability and it has the added advantage of identifying species of more mosquito genera. Since the RBFN computational method designed for species classification involving reported NCBI data base has shown effective classification efficiency, the method is expected to perform well for other data sequences if their analogues are involved in training.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No Animals/Humans were used for studies that are base of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors report no conflicts of interest. The authors alone are responsible for the content and writing of the paper.
ACKNOWLEDGEMENTS
Decleared none.
APPENDIX A
RBFN Algorithm
In RBFN, the nodes in hidden layer represent radial basis functions (RBFs), which are characterized by the following:
(i) A center vector mi in the input space, made up of cluster centers with elements mij (j = 1 to n).
(ii) A distance measure to determine how far an input vector I, with elements Ij (j = 1 to n), is from the center vector mi as defined by
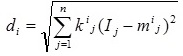 |
(A.1) |
where kij is the (i,j) th element of the shape matrix K defined as the inverse of the covariance matrix:
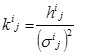 |
(A.2) |
where hij is the correlation coefficient, and σij represents marginal standard deviation.
(iii) A Gaussian type of transfer function which transforms the Euclidian summation di (i = 1 to m), to give an output for each node as defined by
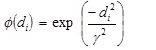 |
(A.3) |
where γ is a real constant.
The hidden layer processes the output from the input layer using the distance measure of Eq (A.1) and the transfer function of the form given in Eq (A.3). The output of the network is a weighted sum of the outputs of ϕ (di) from the hidden layer, i.e.
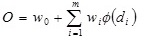 |
(A.4) |
Automatic Configuration of RBFN
An efficient algorithm, namely, hierarchically self-organizing learning (HSOL) algorithm is used to automatically configure the RBFN. The HSOL algorithm automatically creates RBFs and adjusts parameter vectors of the RBFN. Further details concerning the HSOL algorithm can be referred elsewhere [34], [37], [38].
A simple way of measuring the progress of learning for a single output network is by defining the root mean square error, Erms for N teaching patterns
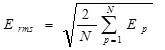 |
(A.5) |
with
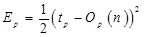 |
(A.6) |
where tp represents the desired output value defined by the pth teaching pattern, Op represents the actual output value of the pth teaching pattern, and n represents a column vector which is a collection of all parameters associated with the output. The parameter saturation vector s is defined as
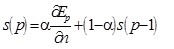 |
(A.7) |
where α is a positive constant between 0 and 1, and p represents the p th teaching pattern presented to the network. The vector s provides the weighted average of (∂Ep / ∂n) over the horizon of learning iterations. The saturation criterion ρ is defined by the integration of the inverse of 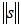 as
as
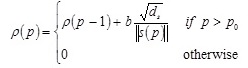 |
(A.8) |
where ds is dimension of s, b is small positive constant representing the increment rate of ρ, and p0 is the delay factor defined as 1/α.
The network parameter update rules are derived from the negative gradient of the error function, Eq. (A.5).
The weights between the output and the i th RBF, wi:
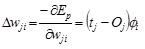 |
(A.9) |
The j th element of the mean vector, mi
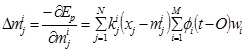 |
(A.10) |
The marginal standard deviation,σ ij:
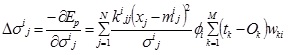 |
(A.11) |
The correlation coefficient, hijk:
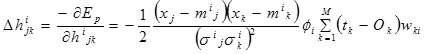 |
(A.12) |
The parameter vector of the output unit,
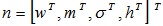 is updated by
is updated by
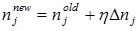 |
(A.13) |
where η is the positive constant called the learning rate, and 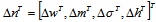 .
.
APPENDIX B
The mean squared error (MSE) is defined as
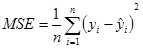 |
(B.1) |
where yi and ŷ andare the target and predicted species output values and n is the number of data sequences used for prediction.
The correlation coefficient (R2) is defined as
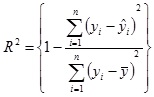 |
(B.2) |
where 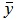 is the mean value of target measurements used for prediction.
is the mean value of target measurements used for prediction.


