All published articles of this journal are available on ScienceDirect.
Genetic Expression in Biological Systems: A Digital Communication Perspective
Abstract
The transcription and translation of Deoxyribonucleic Acid (DNA) involve the processing of genetic information (adenine, thymine, guanine, and cytosine), which can be interpreted as the processing of discrete signals. Additionally, the proper transmission and reception of proteins can be understood with typical theories of digital communication systems. Thus, concepts as routing, error control, and Shannon’s theorem may be the equivalence to determine a target organ, the maturation in the primary transcript molecule of Ribonucleic Acid (RNA) messenger, and the regulation of gene expression (that defines the development of multicellular organisms), respectively. Due to the high performance of transmitting information shown by typical digital communication systems, modeling the analogies between biological communication systems and digital communication systems as mentioned above may allow overcoming the challenges that biological systems face and having more efficient treatment of lethal diseases such as cancer.
1. INTRODUCTION
The Information and Codification Theories (ICTs) show significant parallels between traditional communication systems (electronic or optical) and biological communication systems [1]. Thus, analyzing the functions of such systems through ICTs establishes equivalences between them, allowing a duality in the use of mutual principles of information transmission. Biological systems can detect the presence of components that allow them to perform transmission. At the origin, there is a source of information where the data are represented by particles or molecules (stored in that source through a physical process). These particles are emitted to a communication medium the propagation of which to the receiver is based on physical-chemical mechanisms. At the receiving end, the particles are quantified by parameters such as presence/absence, their concentration in time and/or frequency, and their different types [2]. It is important to note that in living beings, the transmission of information is required to communicate the presence of diseases. Fortunately, disease-treating medicines also use information-transmission processes to counteract these anomalous messages [3].
On the other hand, the principles of transmission used in conventional communication systems are also used in biological systems. In this way, for instance, the theories of computer network administration (monitoring and control) can be applied to biomolecular networks to locate organs affected by diseases and determine their pertinent medical treatment [4]. In this sense, error-correction codes used in digital communication systems to confer reliability on transmission and/or storage are used in biological communication systems for the transmission and storage of genetic codes [5]. In a study [6], the mathematical characterization of a model of biological cell communication and its similarities with a digital communication system are presented aiming at identifying sequences of Deoxyribonucleic Acid (DNA).
This article proposes to model gene expression as a digital communication system since digital communication constitutes one of the most efficient technologies for information processing and transference. Such advantages, when applied to the medical field, could improve the quality of life of human beings employing a new paradigm for the treatment of diseases. The communicational model to be taken into account is the model that was established by Shannon [7], where the transmission model of information is based on channels with noise in which the molecular transmissions also fit.
The remainder of this paper is organized as follows. Section 2 digitally models the biological principles of transcription and translation of DNA and its use in cell receptors. This section also analyses the capacity (maximum speed transmission) of the biological communication channel (blood flow) for a case in which genetic synthesis produces peptide hormones. Finally, Section 3 draws the conclusions.
2. DIGITAL MODEL OF GENE EXPRESSION
2.1. Digital DNA Transcription Model
We consider that the nucleus of a cell can be a biological Data Terminal Equipment (DTE) which contains DNA molecules as an information source (i.e., the transmitter). DNA organizes genetic information into nucleotide blocks called genes. A gene is usually defined as a set of nucleotides that stores information that allows a protein or RNA (ribonucleic acid) to fulfill a biological function in some target organs [8]. Thus, for digital systems, the content of a gene includes information that directs it towards its receiver [1]. Addressing (or routing in digital systems) is also essential in biological systems because it allows the system to unequivocally identify the target organ to which the information will be transmitted for the completion of a biological function in the human body (which is beneficial in medical treatments that allow, for instance, the timely identification of tumor cells). The DNA content represents digital information, as it consists of four discrete values that denote the four types of nucleotides. A nucleotide is a monomer or subunit of nucleic acids (DNA or RNA) and is composed of a nitrogenous base, a chain of five sugars and a phosphate group. There are five nitrogen bases: Adenine (A), Thymine (T), Cytosine (C), Guanine (G), and Uracil (U).
At the beginning of transcription, an enzyme called RNA polymerase II (RNAP) recognizes a region in the DNA sequence known as the promoter, which contains information for the initiation of transcription. Next, RNAP merges nucleotides to form complementary sequences of messenger RNA (mRNA) into a single chain of biological information that is identical to that of DNA except for the replacement of thymine by uracil. Another element that is present in the DNA sequence is the so-called enhancer, which is responsible for regulating the amount of mRNAs produced and are sent to a biological receptor [9]. Digitally, the action performed by the enhancer can be considered to be a flow control mechanism, a mechanism used by the receiver to manage the amount of information that a transmitter communicates [2, 10]. At the end of transcription, the primary mRNA molecules are matured via the following modifications [11]: splicing, placement of a cap, and placement of a poly-A tail which can be considered as an error control mechanism in digital communication systems.
2.2. Digital DNA Translation Model
Once transcription ends, the genetic information should be transmitted from the DTE to the Digital Communication Equipment (DCE). In a conventional communication system, this connectivity takes place using a physical interface. In molecular systems, this connectivity occurs in the cytosol [1] From our perspective, the ribosomes and Endoplasmic Reticulum (ER) represent the DCE because these organelles provide a functional structure (or the appropriate format) to the genetic information so that it can travel via biological transmission and reach the receiver. The biological information is appropriately formatted during the process of genetic translation, in the form of chains of amino acids with functions inside the cell (autocrine system) or outside the cell (paracrine and endocrine systems). Thus, the biological DCE encodes information via translation by associating a specific input sequence (data in the mRNA) with a specific output sequence (amino acid chain). This process can be analogized to the codification of data in communication systems [1]. Subsequently, proteins are transmitted through an endoplasmic membrane.
2.3. Biological Propagation of Information on the Transmission Channel
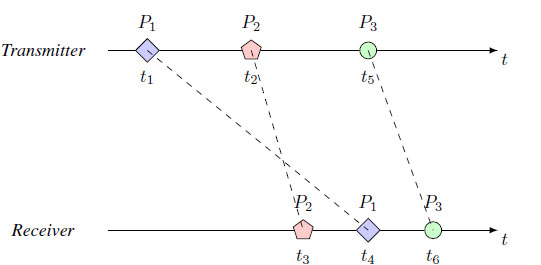
We will briefly refer to protein-type hormones that are excreted by transmitting cells and are transported through the bloodstream to reach a target organ (endocrine system) to communicate between distant cells. This type of transport follows the physical laws of Fick and Brownian-type movement of particles for the transmission of fluids with drift. As in conventional communication systems, in the bloodstream, the information signal is also degraded because of the coverage distance of the transmission and the noise. This is due to the behavior of random-origin biological particles and unwanted chemical reactions among the molecules. For instance, Fig. (1) illustrates the particles P1, P2, and P3, arriving at different times (i.e., in different order) from the transmitter to the receiver [12]. The communication problems, as mentioned earlier, can cause latency, jitter, increase losses, and also Inter-Symbol Interference (ISI).
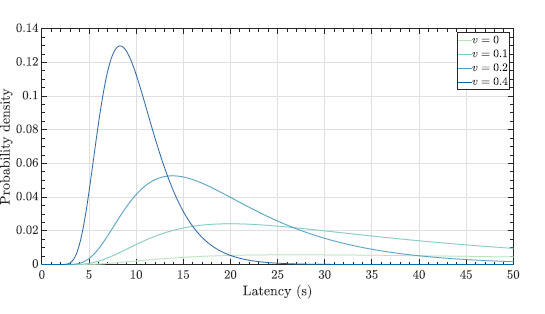
Fig. (2) represents the propagation of molecules in a flow with drift [13, 14] that follows
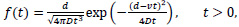 |
(1) |
Where v ≥ 0 represents the drift velocity of the fluid, D is the diffusion coefficient of the molecule, and d is the distance from the transmitter to the receiver.
Based on the communicational parameters that denote the problems that can occur in a communication channel with noise, the Shannon theorem [7] is used to determine the maximum biological information transfer speed (capacity of a channel) as [15]
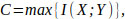 |
(2) |
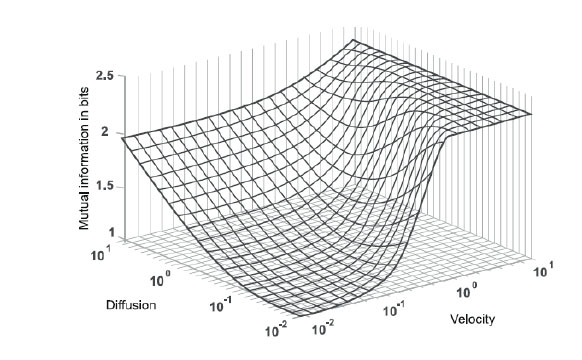
where I(X ; Y) represents the entropy of mutual information (MI) of X and Y. The information signals at the transmission and reception ends are denoted as X and Y, respectively. In Fig. (3), the result of the application of the Blahut-Arimoto algorithm to maximize the MI is shown. By this method, the biological transmitter sends a particle in each transmission slot. Also, in Fig. (3), mutual information (measured in bits) is displayed in relation to the diffusion constant and velocity or drift of the fluid.
In addition, the MI increases with the increase in velocity and reaches its maximum value at log2(N), where N equals the number of transmission slots. If a transmitter does not send any molecule in any transmission slot, then the maximum value of MI will be log2(N + 1). It is also notable that when the velocity values are high, the MI values do not depend on diffusion coefficient changes [15].

2.4. Use of Information at the Receiver
In the molecular receiver, the information is processed through a structure formed by a ligand-receptor which acts as a transducer that decodes the received signal (acting as DCE). It is responsible for several biochemical reactions within the target cell or organ to fulfill a biological function in the body (acting as DTE) [16]. Thus, this biological transmission can be compared to that of the extreme-to-extreme type that is carried out in digital communication systems [1]. In Fig. (4), the proposed biological model is summarized, highlighting the contrasts with Shannon’s communication model.
CONCLUSION
We proposed a model of gene expression through a digital communication system. In this model, the transmitter is composed of DTE (the cell nucleus containing DNA as a source of information) and DCE (ribosomes and the endoplasmic reticulum) on the transmitter side. Shannon’s theorem allows determining the maximum velocity of the transfer of biological information (propagation of hormones in the endocrine system) through the bloodstream (channel of transmission with noise). With values equal to or less than the maximum information transfer rate, successful transmission can occur even though the propagation channel is noisy or has limitations. At the receiving end, the biological information is captured by hormone target cells that decode the received signal (acting as DCE), causing various biochemical reactions within the cell or target organ to fulfill a biological function in the body (acting as DTE). This model could be used in the medical field through a communicational understanding of the functioning of biological systems, in which the advantages of digital systems can be applied in terms of efficient processing and transmission of information. It would boost the development of more advanced medical treatments that are less aggressive and have fewer side effects. Thus, the proposed model introduces a new approach for the treatment of lethal diseases and the radical improvement of the quality of life of humans. As future work, we have planned to use a simulated environment of information transmission networks at the biological level for expression through a digital communication system.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of this study are included in the article.
FUNDING
This work was supported by Universidad Nacional de Chimborazo under Grant CONV.2018-ING004.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declare none.


