Solving the increasing reliability and strength, reducing energetic and economic problems by creating modern materials and construction is an urgent scientific task. In the area of structural materials, these problems have been posed, and methods for their solution are well developed; however, using natural bio-composite materials, which include bone tissue, was not sufficiently studied in the rheological deformation area [1, 2].

The problem of increasing the strength characteristics of bone tissue is solved in various ways, one of which is preventive reinforcement with metal implants to reduce stress concentration. Potential prospects for the application of this approach are based on reducing the cost of treatment, reducing the likelihood of fracture, simplicity of the operation compared to the operation of bone fusion after a fracture, short duration of postoperative procedures, etc., [3, 4].

To implement this method, an integrated approach from medicine, mathematics, mechanics, and information technology is required. However, at present, there are no adequate methods of mathematical modeling of the stress-strain state of bone tissue in the process of rheological deformation to analyze and decrease the level of stress concentration in the most loaded areas. There are no appropriate information technologies and software for solving this class of problems as a consequence [5-11].

The surgical methods in the treatment of patients with joint pathology are dominated. The percentage of complications and unsatisfactory results reach 30-40%, which negatively affects the quality of the patient’s life. In recent years, to improve the methods of operations, mathematical modeling has been used. One of the advanced technologies for structural analysis of the stress-strain state of bone tissue is the finite element method. The bone cross-sections models in stress-strain state studies of the hip joint, as a rule, are used. However, they did not take into account the complex structure of the bone material, which did not fully reflect the stress-strain state of the integral structure and allowed the determination of optimal surgical tactics [12-18]. Also, the method of finite differences is widely used to obtain the numerical solution of mathematical models of physical processes. It involves discretization of the area and larger computing resources, but it is easier to implement compared to the finite element method. In particular, the application of this method is shown [19, 20].

This type of injury is a particular problem in patients over 60 years of age. Prolonged immobilization (more than 14 days) in such patients causes a sharp deterioration of movement functions and decreases the potential for restoration of movements to the minimum of a necessary physiological rate. Despite the maximum objectivity of the physical experiment, it is impossible to repeat the experiment on the same material due to stress overloads and after its complete or partial destruction. Mathematical modeling or numerical experiment is devoid of these drawbacks [1, 3].

The problem of determining the mechanical characteristics of bone tissue in elastic, elastoplastic (nonlinear) areas under short-term loads and the area of ​​creep of this material under long-term power loads remains unresolved. The complex structure of bone tissue, insufficient experimental material, changes in bone characteristics with age complicates the process of determining its mechanical and rheological characteristics. In addition, it can be seen from experimental experiments that stretching loads is 1.5 times more dangerous than compression (i.e., fracture under tension occurs at stress intensities 1.5 times lower than at stress intensities during compression) [21, 22].

It is impossible to describe the processes of destruction of bone tissue using only the features of linear elasticity theory. Using the nonlinear model of the biomaterial behavior under short-term loads in calculations is rare. Bone can rebuild over time depending on the load, so this material should exhibit the effects of creep and stress relaxation under prolonged static loads [8, 23].

Investigation of the symmetric properties of differential equations containing fractional derivatives is currently an urgent scientific problem in connection with the increased use of such equations in mathematical models of various processes with anomalous kinetics. Moreover, in contrast to the classical derivative of integer order, there are many non-identical definitions of derivatives of fractional order, which leads to a variety of differential equations of fractional order that are close in form but significantly different in properties [24-33].

Biomaterials, in particular bones, have a porous, heterogeneous structure and a complex nature of spatial correlations. The rheological behavior of these materials is not linear. In particular, it is possible to distinguish the presence of memory effects that significantly affect the development of stresses and strains during reloading. Based on the structural and rheological properties of bones, this biomaterial can be attributed to materials with a fractal structure. Using the mathematical apparatus of integro-differentiation of the fractional-order in the construction of mathematical models of rheological behavior of biomaterials will allow us to take into account their complex nature of spatial correlations, the presence of memory effects, self-organization, and deterministic chaos [14].

In this section, the basic relations of the linear elasticity problem of biomaterials while taking into account their fractal structure are received. The principle of virtual works at small deformations and the mathematical apparatus of integro-differentiation of fractional order to obtain a variational formulation of the problem are used. The finite element method with a piecewise linear basis to find the minimum of the obtained energy functional was used. The UML diagram of the developed software for finding the components of the stress-strain state of the biomaterial subjected to external loading was given.

2.1. Some Properties of Integrals and Derivatives of Fractional Order

Following the main properties of the fractional-order integro-differentiation apparatus, it seems promising to use the theory of fractional calculus in the study of mechanical processes and phenomena in natural and artificial inhomogeneous structures, biomaterials, and nanomaterials.

(1)

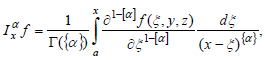(2)

Let us consider the fractional-order integro-differentiation operators integral of the function f(x,y,z) over the variable x in Caputo's understanding in more detail [27, 34, 35].

Where 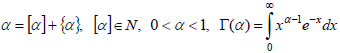- gamma function.

Repeated use of the fractional-order operator to the function is equivalent to one-time using of the fractional operator when its order is equal to the sum of orders [27, 34]:

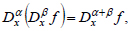(3)

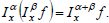(4)

The action of a fractional operator on the sum of functions is equivalent to the sum of actions of the fractional operator on each of the functions [27, 34]:

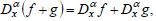(5)

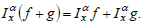(6)

The action of the fractional operator on the product of the constant c and the function f is equal [27, 34]:

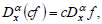(7)

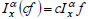(8)

Provided that 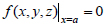the following property is valid [27, 34]:

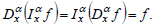(9)

During constructing the variational formulation of the linear elasticity problem, many operations related to the combined application of integration and differentiation operators are performed. To construct a variational formulation of the linear elasticity problem of biomaterials with a fractal structure, the formulation of fractal operators in the Caputo understanding was chosen based on a property (9). At the initial moment of modeling time, the biomaterial is in a natural stress state, i.e., there are no stresses and displacements. If at the initial moment, the body is not in a natural stress state, then property (9) will not be valid. The history of stresses and displacements must be taken into account during the combining application of fractional integration and differentiation operators. The Caputo formulation of fractional operators allows us to take into account that fact.

2.2. The Linear Elastic Deformation Problem

The calculation of the mechanical behavior of biomaterial for a given dependence of loading by time is based on an adequate mathematical model of the properties of a material with the fractal structure. For biomaterials, such model is based on fractional derivatives, which take into account the loading mode and existing effects of memory, spatial non-locality, self-organization, and deterministic chaos in the material. The expediency of using the mathematical apparatus of integro-differentiation of fractional order to build mathematical models of physical processes in environments that are characterized by such properties has been described [14, 28]. Rabotnov Yu.N. was engaged in the construction of mathematical models of the elasticity theory for medium with after-effect. He also showed the feasibility of using such mathematical apparatus in the model’s creation and its advantages over the traditional approach [14, 23].

Let us consider the problem of stress-strain state in biomaterial taking into account the fractal structure. Suppose that a body that is in equilibrium is affected by mass forces 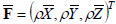in the corresponding directions, and also surface forces 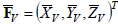with corresponding projections on the axis x,y,z. Let us find the components of the stress-strain state of the body, namely vectors 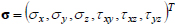- stress, 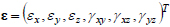- deformation and displacement 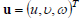, which are satisfying the equilibrium equation in elementary volume [36-38]:

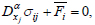(10)

and the equilibrium conditions on the surface [39]:

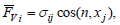(11)

where n- outer normal to the surface of the body S.

Taking into account the fractal structure of biomaterials, relations between displacements and deformations can be written in the following form [39]:

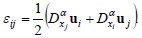(12)

Hooke's law makes it possible to express stress due to deformation and vice versa [8, 9, 14, 23]:

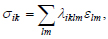(13)

where, σ_ik - stress tensor, ε_lm - deformation tensor, λ_iklm - elastic modulus tensor.

We introduce a notation to simplify the further description of the material:

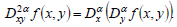(14)

Considering (12), the ratio of the deformation community in a biomaterial with a fractal structure will be as follows [39]:

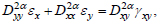(15)

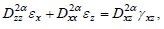(16)

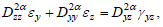(17)

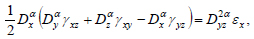(18)

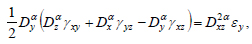(19)

(20)

Thus, the obtained relations make it possible to describe the rheological behavior of a biomaterial with a fractal structure under the action of an external load.

2.3. Variational Formulation of Linear Elastic Deformation Problem

In the process of deformation of the system, the energy accumulates in their element, which is called the potential energy of deformation. It is equal to the actual work of internal forces, and it is considered positive. In flat systems, the potential energy of deformation consists of the energy of tension-compression, bending, and shear.

All general theorems for small deformations are based on the equation of virtual works [36, 40]:

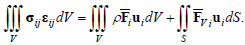(21)

where V - body volume, S - body surface.

Thus, among all permissible displacements u,υ,ω that satisfy the boundary conditions, the active displacements result in a stationary of full potential energy and provide a minimum of functional Π

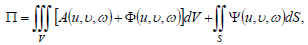(22)

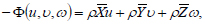(23)

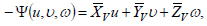(24)

where A(u,υ,ω) - the strain energy function can be written in the form:

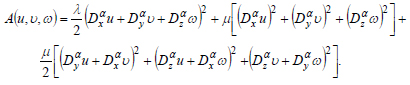(25)

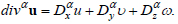(26)

Substitute the expression of stresses due to deformations from the relations (4)-(9). Then, taking into account relation (3), the equilibrium conditions on the surface due to displacement were obtained:

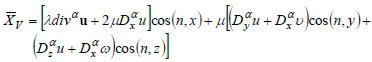(27)

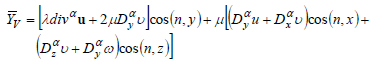(28)

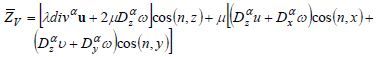(29)

Thus, a variational formulation of the elastic deformation problem of biomaterials with a fractal structure was obtained.

2.4. Finding the Minimum of Full Energy Functionality

Let us construct full potential energy functional for a one-dimensional problem of the linear elasticity theory of a biomaterial with a fractal structure:

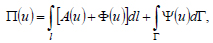(30)

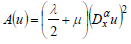(31)

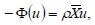(32)

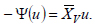(33)

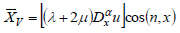(34)

Using Stoke’s formulas, we obtain:

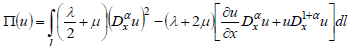(35)

Let us find an approximate solution of the minimum of full potential energy functional in the following form:

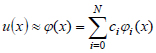(36)

Inserting (36) in (35), we obtain:

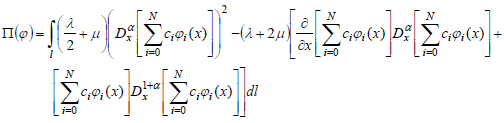(37)

Using properties (7) and (8) from (37), we can obtain:

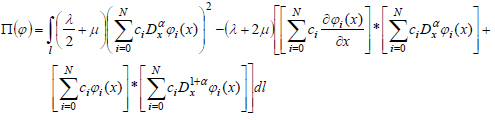(38)

We use the necessary condition for the existence of the extreme to find the minimum of the full potential energy functional:

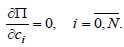(39)

The differential of full potential energy functional by variables 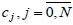can be written as:

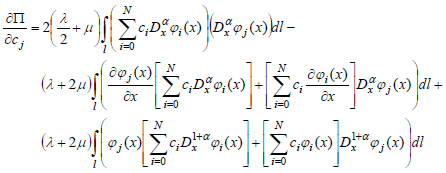(40)

Thus, we obtain a system of linear algebraic equations with unknown variables 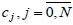. Having solved it, we obtain the values 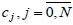and put them into the relation (36). As a result, we obtain a function that gives a minimum of the full potential energy functional (30).

2.5. Using a Piecewise Linear basis for Finding the Minimum of the Full Potential Energy Functional

Let us divide the segment [a,b] into a uniform grid into N parts:

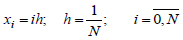(41)

We choose as a basis for (36) the piecewise linear functions having the following form [13]:

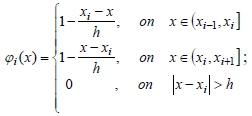(42)

Let us find the derivatives of basis functions (42).

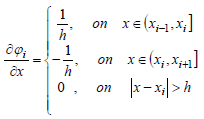(43)

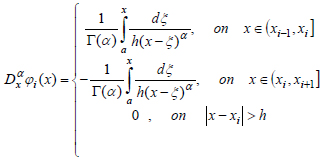(44)

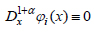(45)

Substitute the obtained relations (42-45) into the expression (40):

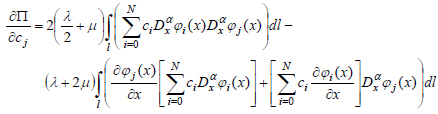(46)

Taking into account (43), the equation (46) will be written as:

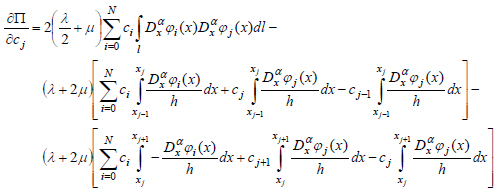(47)

Equating relation (47) to 0, we obtain a system of linear algebraic equations with unknown variables 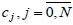Solving and substituting the basic functions (42) and the found coefficients 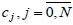in relation (36), we obtain the required displacements. Substituting the found displacements into the relation (12), we obtain deformations. Substituting the found deformations in (13), we obtain the required stresses biomaterial while considering its fractal structure.

We conduct a numerical experiment for the cross-section of the femur bones with a diameter of 2 cm of an 80 years old person. Let us consider a one-dimensional case. So, 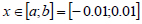. Let us fix the sample on the boundary a, so we can formulate the boundary condition on this boundary as 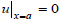. Let us force the load 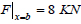to the opposite side of the material. Using the developed software and formulated variational statement of the linear elasticity problem for a biomaterial with a fractal structure, we calculate the components of the stress-strain state of the described sample under the action of external load.

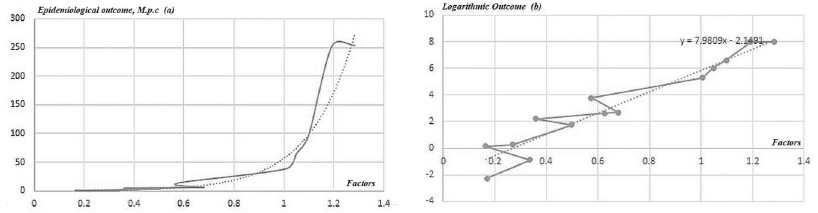
The curves in Fig. (2) show that the nonlinear part begins to be observed at deformation values ε ≥ 0,237%. Considering the fractal structure of bone material makes it possible to take into account the effects of nonlocality and the complex nature of spatial correlations. Analyzing the obtained results, we can conclude that the fractal structure contributes to the accumulation and “memorization” of the stress state of the material. The graphical dependences show that the difference between stresses while taking into account the fractal structure of the material and without at deformations ε ≥ 0,8% exceeds 4.8%.

Fig. (3 ) shows the stress distribution in the sample depending on the spatial coordinates. Analyzing the obtained results, we can conclude that the maximum stresses σ ≈ 15 MPa will be relatively small from the fixed boundary of the sample. However, on the opposite side, the maximum stresses are significantly higher. Taking into account the fractal structure of the material, the maximum stresses are equal to σ = 153 MPa. Considering the traditional model α = 1 the maximum stresses are equal σ = 141 MPa.

Consider the deformations in this sample while taking into account the fractal structure of the material and without, after applying the different loads on its boundary. Curve 1 and Curve 2 describe the deformations in the sample at the boundary b under loads F = 35 MPa, and Curve 3 and Curve 4 under loads F = 57 MPa.

Fig. (1). Class diagram of developed software for finding the numerical solution of elastic deformation problem of biomaterials with fractal structure.

Fig. (2). Changing of the stress component σx depending on deformation while taking into account the fractal structure of biomaterial and without

Fig. (3). The value of the stress component σx depends on the spatial coordinate while taking into account the fractal structure of biomaterial and without

Fig. (4). The value of the deformation component εx depending on the time at different loads while taking into account the fractal structure of biomaterial and without

After analyzing the results obtained from Fig. (4), we come to the following conclusion. In the initial moments, there is an elastic deformation that is visible in Fig. (4). The complex structure of the material determines the presence of a nonlinear component of the deformation process. In the case of Curve 1 and Curve 2, the deformations develop more slowly, which is explained by the smaller value of the applied load in comparison to Curve 3 and Curve 4. Taking into account the fractal structure has a more significant effect on the results at higher loads. In particular, in the time interval t ϵ (0,60) the deformations while taking into account the fractal structure of the material will be smaller (the maximum difference between Curve 3 and Curve 4 in this range is 14.3%). In the time interval t ϵ (60,100) the deformations while taking into account the fractal structure of the material will be greater (the maximum difference between Curve 3 and Curve 4 in this range is 6.8%). This effect can be explained by the presence of stress memory in the material, which causes the accumulation of residual stresses.

Using the basic laws of mechanics of hereditary environments and the mathematical apparatus of integro-differentiation of fractional order, new mathematical models of elastic deformation of biomaterials with the fractal structure were obtained, which allows taking into account the existing effects of memory, spatial non-locality, self-organization and deterministic chaos in the material.

The basic equations of the elastic deformation problem of biomaterials while taking into account their fractal structure were obtained. A variational formulation of this problem was constructed, which allows obtaining an approximate continuous solution of the problem. The finite element method with a piecewise linear basis for finding the solution to this problem was used.

Application software for finding an approximate solution of the elastic deformation problem of biomaterials while considering their fractal structure was developed. The class diagram of the developed software was built.

The components of the stress-strain state of the femur bones subjected to different external loads considering the fractal structure of the material and without, were found. The analysis of the obtained results showed that using the apparatus of integro-differentiation of fractional order in the construction of mathematical models of the linear elasticity theory allows calculating the residual stresses in the material.