All published articles of this journal are available on ScienceDirect.
Adaptive Probabilistic Neuro-Fuzzy System and its Hybrid Learning in Medical Diagnostics Task
Abstract
Background:
The medical diagnostic task in conditions of the limited dataset and overlapping classes is considered. Such limitations happen quite often in real-world tasks. The lack of long training datasets during solving real tasks in the problem of medical diagnostics causes not being able to use the mathematical apparatus of deep learning. Additionally, considering other factors, such as in a dataset, classes can be overlapped in the feature space; also data can be specified in various scales: in the numerical interval, numerical ratios, ordinal (rank), nominal and binary, which does not allow the use of known neural networks. In order to overcome arising restrictions and problems, a hybrid neuro-fuzzy system based on a probabilistic neural network and adaptive neuro-fuzzy interference system that allows solving the task in these situations is proposed.
Methods:
Computational intelligence, artificial neural networks, neuro-fuzzy systems compared to conventional artificial neural networks, the proposed system requires significantly less training time, and in comparison with neuro-fuzzy systems, it contains significantly fewer membership functions in the fuzzification layer. The hybrid learning algorithm for the system under consideration based on self-learning according to the principle “Winner takes all” and lazy learning according to the principle “Neurons at data points” has been introduced.
Results:
The proposed system solves the problem of classification in conditions of overlapping classes with the calculation of the membership levels of the formed diagnosis to various possible classes.
Conclusion:
The proposed system is quite simple in its numerical implementation, characterized by a high speed of information processing, both in the learning process and in the decision-making process; it easily adapts to situations when the number of diagnostics features changes during the system's functioning.
1. INTRODUCTION
Data mining methods are currently widely used in the analysis of medical information [1-3] and, first of all, in diagnosis problems based on the available data on the patient's state. As a rule, medical diagnostics problems from a data mining standpoint are considered either problems of pattern classification-recognition, clustering - recognition without a teacher, or forecasting-prediction of the disease course. Methods of computational intelligence [4-7] adapted for solving medical problems [8-11] proved to be the best mathematical apparatus here. Artificial neural networks have proved to be efficient [12] due to their ability to train parameters - synaptic weights (and sometimes architecture) to process a training dataset, which ultimately allows or restores distributing hyper surfaces between classes of diagnoses arbitrarily shapes. Here deep neural networks have effectively demonstrated their capabilities [13, 14], which provide recognition accuracy entirely inaccessible for other approaches.
Simultaneously, there is a broad class of situations when deep neural networks are either ineffective or generally inoperable. Here, notably the problems with a short training dataset often happen in real medical cases. Also, medical information is often presented not only in a numerical scale of intervals and relationships but also in a nominal, ordinal (rank) or binary scale.
Probabilistic Neural Networks (PNNs) [15, 16] are well suited for solving recognition-classification problems under conditions of a limited amount of training data [17], which, however, are crisp systems operating in conditions of non-overlapping classes and learning in a batch mode. In previous works [18-22], fuzzy and online PNN modifications were introduced to solve recognition problems under overlapping classes and trained in sequential mode. The main disadvantages of these systems are their cumbersomeness (the size of the training dataset determines the number of nodes in the pattern layer) and the ability to work only with numerical data. The ability to work with data in different scales is an advantage of neuro-fuzzy systems [23]. Here, for the problem under consideration, ANFIS, Takagi-Sugeno-Kang, Wang-Mendel and other systems can be noted.
Unfortunately, training these systems (tuning their synaptic weights, and sometimes membership functions) may require relatively large amounts of training datasets [24]. In this regard, it seems expedient to develop a hybrid of a Probabilistic Neural Network (PNN) and a neuro-fuzzy system for solving classification-diagnostics-recognition problems in the conditions of overlapping classes and training data in different scales, as well as the ability to instantaneous tuning based on lazy learning [25].
In a study [26], the adaptive probabilistic neuro-fuzzy system for medical diagnosis was introduced. On its outputs, the probabilities
Due to this, it is an adequate representation to consider the diagnostic procedure as fuzzy reasoning [4-7, 23]. Here alongside the probabilities
2. MATERIALS AND METHODS
2.1. Architecture of Fuzzy-probabilistic Neural Network
The proposed probabilistic neuro-fuzzy system (Fig. 1) contains six layers of information processing: the first hidden layer of fuzzification, formed by one-dimensional bell-shaped membership functions, the second hidden layer - aggregation one, formed by elementary multiplication blocks, the third hidden layer of adders, the number of which is determined by the number of classes plus one per which should be split the original data array, the fourth - defuzzification layer, formed by division blocks, at the outputs of which signals appear that determine the probabilities of belonging
Unlike classical neuro-fuzzy systems, there is no layer of tuning weights parameters. As will be shown below, the proposed method's learning process is implemented in the first hidden layer by adjusting the membership functions' parameters. It is clear that this approach simplifies the numerical implementation of the system and improves its performance, especially under conditions of a short training dataset.
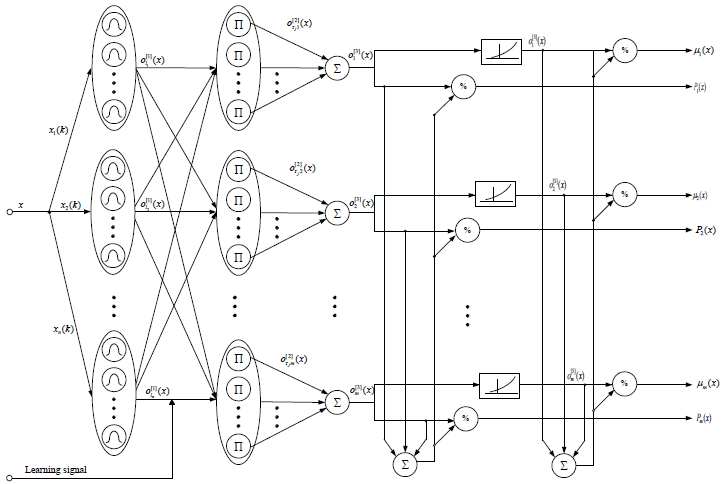
The initial information for the system synthesis is a training dataset formed by a set of n-dimensional images-vectors
Based on this training dataset, the first hidden fuzzification layer is formed by Gaussian membership functions.
 |
(1) |
Where
Note that in a standard probabilistic neural network, the first hidden layer of patterns is formed by multidimensional Gaussians, the number of which is determined by the training dataset size N. In the proposed system, the number of membership functions at each input can be different, for example, if a binary variable of type 1 or 0, “Yes” or “No,” “there is a symptom,” or “there is no symptom,” is supplied to the input then two functions are enough at this input (
 |
(2) |
where h = 
At the input of the first hidden layer h signal-values of the corresponding Gaussians appear.
 |
(3) |
Then they are fed to the second - aggregation hidden layer, which, similarly to standard neuro-fuzzy systems, is formed by ordinary multiplication blocks which are equal to N.
In this layer from one-dimensional membership functions, the multidimensional kernel activation functions are formed:
 |
(4) |
the vector centres of which
 |
(5) |
The third hidden layer is formed from the blocks of summation, the number of which is determined by the value m + 1. The first m adders calculate the data density distribution for each class:
 |
(6) |
and (m+1)-th one overall data density distribution.
 |
(7) |
In the fourth layer, the probability level is calculated that the presented observation x belongs to the j-th class.
 |
(8) |
In the fifth hidden layer, the nonlinear transformation is implemented with a nonlinear activation function.
 |
(9) |
and, finally, in the output layer, levels of fuzzy membership with soft max function are calculated:
 |
(10) |
Satisfying of obvious condition:
 |
(11) |
A combined training of probabilistic neuro-fuzzy system In general, the proposed system's settings can be implemented based on the so-called lazy learning [25] in the same way a standard PNN is configured. Lazy learning is based on the principle “Neurons at data points”, when the kernel activation functions' centers coincide with the observations from the training set. For each observation
Following this approach, N membership functions should be formed at each input in a neuro-fuzzy system in the first fuzzification layer. However, suppose the training signals on different inputs are specified either in the nominal or binary or in the rank scales, in this case, the number of membership functions at the corresponding inputs decreases significantly. In addition, in medical applications, numerical variables, such as the patient's temperature, are often repeated, leading to the conjugation of the number of membership functions. Finally, the most straightforward case compensates when all input signals are specified in a binary scale: “there is a symptom” – “there is no symptom”. Only two membership functions with center coordinates 0 and 1 are formed at each input.
In the case when all the input variables are specified on a numerical scale, the number of one-dimensional membership functions is determined by the value.
Let us set the maximum possible value of the number of membership functions at the i-th input
 |
(12) |
When the first vector from the training dataset is fed to the system input
 |
(13) |
 |
(14) |
After this center “winner” is pulled up to the input signal
 |
(15) |
where
At the k-th iteration, the tuning procedure can be written in the form represented with formula 16.
 |
(16) |
It is easy to see that the last expression implements the self-learning principle of T.Kohonen [27] “Winner Takes All” (WTA).
Thus, the combination of lazy learning and self-learning can significantly simplify both the architecture and the process of tuning the probabilistic neuro-fuzzy system.
3. RESULTS
The proposed probabilistic neuro-fuzzy system is designed to work with different data types, such as numerical and binary data that are presented in long and short datasets. Therefore, two datasets with different data types were taken from the UCI repository for the experimental evaluation.
The first dataset, “Heart Disease,” contains 303 instances and 76 attributes, but only a subset of 14 of them is used. Each observation includes detailed information about the patient, his or her physiological parameters, and symptoms of a disease. This dataset is a mix of numerical and binary data. Physiological parameters have numerical form, and symptoms typically have a binary form.
The purpose of this dataset is to find out whether the patient has the disease or not, which value between 0 and 4, where 0 is the absence of disease. Also, this dataset contains overlapping classes, as shown in Fig. (2).
The second dataset, “Diabetes 130-US hospitals for years 1999-2008”, is a long dataset that contains 100000 instances. It includes features that represent outcomes of treatment for patients: the length of stay at the hospital, information about the laboratory tests, and medications administered when patients were at the hospital. This dataset also contains numerical and binary data.
The experiment results show that the KNN algorithm is fast, but its accuracy is close to 50%. Thus, the algorithm is not intended for the classification of very short samples. Unlike KNN, the proposed network's classification accuracy increases as the number of elements in the sample increases. Even on very small samples, it achieves an accuracy of 77%. EFPNN also allows for greater accuracy as the sample size increases. However, it is significantly more than 20% slower than the proposed network. The fastest method is KNN, but it should take into account that neural networks are implemented on Python and run on the central processor, and not on the GPU like KNN. It means that with the same hardware implementation, the time costs for all methods will be comparable. But the accuracy of the proposed network is higher (Fig. 3).
The experiment results show that the KNN algorithm is fast, but its accuracy is close to 50%. Thus, the algorithm is not intended for the classification of very short samples. Unlike KNN, the proposed network's (APNFS) classification accuracy increases as the number of elements in the sample increases. Even on very small samples, it achieves an accuracy of 77%. Takagi–Sugeno–Kang Fuzzy Classifier (TSK) and Wang-Mendel systems also allow archiving for greater accuracy as the sample size increases.


| Algorithms for Comparison | Classification Accuracies, % | Max Time | |||
|---|---|---|---|---|---|
| 100 | 150 | 200 | 250 | ||
| KNN | 50.24 | 51,63 | 50.7 | 49.03 | 0.03 |
| TSK | 59.91 | 62.33 | 74.08 | 78.92 | 0.61 |
| APNFS | 52.01 | 57,7 | 69.34 | 77.52 | 0.28 |
From Table 1, it can be seen that the TSK system is slower than the proposed network. The fastest method is KNN, but it should take into account that neural networks are implemented on Python and run on the central processor, and not on the GPU like KNN. It means that with the same hardware implementation, the time costs for all methods will be comparable. But the accuracy of the proposed network is higher.
The second experiment was performed on the long dataset, which is called “Diabetes 130-US hospitals for years 1999-2008”. From the initial dataset, a number of subsets that have different sizes, from 3000 to 30 000 instances, were formed. The experiment is intended to compare the increase of the classification time with the dataset size growth because the absolute time consumption depends on the computer platform and used processor (CPU, GPU). Based on the results of the first experiment, for the second one, two Adaptive probabilistic neuro-fuzzy systems and TSK, which provide higher classification accuracy, were selected. The experiment showed that the proposed approach APNFS requires less computational cost than TSK. The increase in time required for larger subsets increases significantly compared to small subsets. This trend apparently exposes the influence of the software on the classification time. Smaller datasets are usually allocated in RAM, while long datasets require swapping of data from external memory.
Additionally, it is important to mention that the system under consideration outputs not only probabilities of belonging each sample from the dataset to the appropriate class-winner but also levels of membership each observation to all classes. The Breast Tissue dataset from the UCI repository was used to examine the importance of fuzzy reasoning. It contains data describing electrical impedance measurements of recently excised tissue samples from the breast. The dataset has nine features describing such parameters as “distance between I0 and real part of the maximum frequency point”, “a maximum of the spectrum” and others. Also, there are six classes, such as carcinoma, fibro-adenoma, mastopathy, connective, glandular and adipose. The comparison of outputs, both membership levels and probabilities for some patients, is shown in Tables 2 and 3.
| Samples | Level of Membership | |||
|---|---|---|---|---|
| Mastopathy | Carcinoma | Connective | Adipose | |
| Sample 1 | 0.23 | 0.35 | 0.43 | 0.09 |
| Sample 2 | 0.41 | 0.06 | 0.36 | 0.17 |
| Sample 3 | 0.06 | 0.39 | 0.09 | 0.46 |
| Samples | Class-Winner | Probability |
|---|---|---|
| Sample 1 | carcinoma | 0.56 |
| Sample 2 | mastopathy | 0.49 |
| Sample 3 | adipose | 0.61 |
Here we can see that some values of membership levels are quite close one to another; thus, it is important to consider all of them for further diagnostics. Also, it is essential to point out that the usage of just probability values that outputs only one possible diagnosis gives a narrow point of view on the patient’s state, and also, treatment may be less effective.
So, it is better to take into account all possible values, which allow doctors to build further medication processes to do complex, higher-quality treatment.
In general, according to the results of the two experiments, the proposed approach in comparison with TSK provides slightly lower classification accuracy for small datasets but requires significantly lower computational costs when the dataset size grows. Besides that, it is designed to work in online mode on Data Stream Mining tasks.
4. DISCUSSION
In order to solve the problem of classification with data that can be represented in different scales, the adaptive probabilistic neuro-fuzzy system is developed, based on a classical probabilistic neural network, which is able to work under the condition of short datasets. However, PNN’s architecture is growing with training dataset, making it bulky and making the ability to work with long datasets impossible, thus using the self-learning procedure where the distance between centers of membership functions should be “close enough” to form one training observation according to the formula (16), and this is determined by a predefined threshold.
Also, it should be noted that neuro-fuzzy systems allow working with various scales; therefore, to solve the classification-diagnostics-recognition problems, it was necessary to develop a hybrid of such system and PNN making it possible to work under conditions of overlapping classes, data represented in different scales, and the ability of fast tuning system’s parameters based on lazy learning.
However, using only a probabilistic approach can narrow down the perspective on a case, for example, the system gives only one diagnosis for the patient instead of a few of the most possible. Hence, owing to the fact that it is a priory supposed class to overlap in feature space, fuzzy reasoning gives the advantage to this system comparing to the crisp ones.
CONCLUSION
The adaptive probabilistic neuro-fuzzy system is proposed. This system is designed to classify vector observations that are processed in a sequential online mode. It has a limited number of neurons in the fuzzification layer and is characterized by a high rate of learning, which distinguishes it from both deep and traditional shallow multilayer networks and allows for a large amount of data to be processed within the overall problem of Data Stream Mining.
The distinctive feature of the proposed system is combined learning of its parameters and membership functions, combining controlled learning with a teacher, lazy learning based on the concept “Neurons at data points”, and self-learning, which is based on the principle “Winner takes all”. Precisely, this approach allows solving diagnostic tasks in conditions of not just long but also short training datasets and mutually overlapping classes. Thereat, it is important to note that the input information can be given in various notations, in particular: numerical, ordinal, binary, and nominal. In the future, it is reasonable and fascinating to process information in online mode, consider the possibility of data processing, where the size of an input vector varies (appearing or deleting certain features), and a number of possible diagnoses (the appearing of new diseases in data stream under consideration). The computer experiments are proving the proposed approach.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No animals/humans were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
The data supporting the findings of the article is available in the UCI at: https://archive.ics.uci.edu/ml/datasets/heart+disease, reference number [28]. https://archive.ics.uci.edu/ml/datasets/diabetes+130-us+hospitals+for+years+1999-2008, reference number [29]. http://archive.ics.uci.edu/ml/datasets/breast+tissue, reference number [30].
FUNDING
This work was supported by the state budget scientific research project of Kharkiv National University of Radio Electronics “Deep Hybrid Systems of computational intelligence for data stream mining and their fast learning” (state registration number 0119U001403).
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


