Modeling Gene Expression and Protein Delivery as an End-to-End Digital Communication System
Abstract
Introduction:
Digital communication theories have been well-established and extensively used to model and analyze information transfer and exchange processes. Due to their robustness and thoroughness, they have been recently extended to the modeling and analyzing data flow, storage, and networking in biological systems.
Methods:
This article analyses gene expression from a digital communication system perspective. Specifically, network theories, such as addressing, error control, flow control, traffic control, and Shannon's theorem are used to design an end-to-end digital communication system representing gene expression. We provide a layered network model representing the transcription and translation of deoxyribonucleic acid (DNA) and the end-to-end transmission of proteins to a target organ. The layered network model takes advantage of digital communication systems' key features, such as efficiency and performance, to transmit biological information in gene expression systems.
Results:
Thus, we define the transmission of information through a bio-internetwork (LAN-WAN-LAN) composed of a transmitter network (nucleus of the cell, ribosomes and endoplasmic reticulum), a router (Golgi Apparatus), and a receiver network (target organ).
Conclusion:
Our proposal can be applied in critical scenarios such as the development of communication systems for medical purposes. For instance, in cancer treatment, the model and analysis presented in this article may help understand side effects due to the transmission of drug molecules to a target organ to achieve optimal treatments.
1. INTRODUCTION
Communication theories have established an inherent parallel between digital communication systems and biological systems [1, 2]. Thus, the analysis of these systems' behavior based on conventional transmission theories requires the establishment of bidirectional equivalences between them. Undoubtedly, biological systems can be viewed as communication system [3, 4]. They use communication components, such as the sender, channel, and receiver to achieve information transmission. At the sender, the generation or storage of information-carrying molecules requires a physiological process. Subsequently, the information-carrying molecules are released into a channel through which the information-carrying molecules are transported to the receiver due to a propagation mechanism. At the receiver, a detector must be present to measure a particular property or properties of the information-carrying molecules. These properties could be the presence or absence of information-carrying molecules, their concentration, time of arrival, type of molecule, or any other measurable parameter [5].
As mentioned above, the communication model (i.e., transmitter, channel, and receiver) can be used to describe the transmission of malicious information related to human diseases. For example, in viruses, such as the human immunodeficiency virus (HIV), information-carrying molecules propagate through the entire body, causing infection. Fortunately, treatments for diseases and drug transmission systems can provide information that destroys malicious cells. Besides, advanced therapies use gene delivery vectors containing information encoded in DNA to fix unusual or variant genes. Although the information and/or the mechanisms to deliver information may differ among biological systems, the communication model is the same. Thus, communication theories can be used as a foundation for designing a layered protocol platform that combines the advantages of internetworks and computational science to evaluate and model HIV transmission [6].
This paper provides a holistic view of a biological system modeled and analyzed as an end-to-end communication system; concretely, the gene expression is analyzed from a digital communication system perspective. We use network theories, such as addressing, flow control, error control, traffic control, and Shannon's theorem to design layered network models representing the transcription and translation of DNA and the end-to-end transmission of proteins to a target organ. These models take advantage of digital communication systems' key features to transmit biological information in gene expression systems. Further, by analyzing the models, we establish the duality between digital and biological communication systems and provide solutions to overcome the challenges that both systems face. One of the most critical applications of this analysis could be developing communication systems for medical purposes (i.e., disease treatment, such as cancer). For instance, this analysis may avoid side effects by transmitting biological information to a proper destination (i.e., just to a specific target organ) to achieve optimal treatments.
The remainder of this paper is organized as follows. Section 2 reviews the related works on this matter. Section 3 presents an analysis of gene expression and protein delivery based on conventional digital communication systems (i.e., from Shannon's perspective), considering the similarities in the behavior of biological systems and digital systems. Section 4 presents two possible applications of our study in the medical field. Finally, the conclusions of this study are presented.
2. MATERIALS AND METHODS
Several studies in molecular communication [7] focus on diffusion channels' characterization under the physical constraints specific to molecular communication; these constraints are similar to those present in digital communication systems and are even more critical in biological communication systems. This is because these channels are used to deliver information-carrying molecules that play a vital role in the organs of the human body or the administration of drugs to treat disease [8].
In a study [9], a biological system is modeled as a digital communication system. In this biological communication system, nucleotide bases in DNA serve as transmitters, DNA serves as the communication medium, and living organisms serve as the receivers. Errors are hypothesized to occur in the transmission channel and produce mutations in the DNA. The development of robust algorithms that function in one of two regions (i.e., non-protein-coding DNA or protein-coding DNA) is presented as a mechanism to prevent mutations and avoid lethal consequences, such as diseases in biological receivers.
In another study [10], gene expression or, equivalently, biological information flow is presented from an information communication theory perspective and is modeled as a digital communication system. Due to errors in the biological environment (i.e., in the channel), the functions of cells, organisms, or species may be severely affected. However, similarly to digital communication systems, error control and correcting codes can overcome the errors in the transmission medium. In particular, the authors propose linear and convolutional codes to detect and correct errors in a digital representation of gene expression.
The intracellular transmission of genetic information via a biological communication system is represented as a digital communication system [11]. In this biological communication system, the identification, reproduction, and mathematical classification of nucleotide sequences are necessary to identify, reproduce, and mathematically classify DNA sequences subsequently. The errors in the system are efficiently corrected using G linear codes. According to the study in [11], the methodology used to characterize this biological communication system could also be used to prevent mutations in DNA, produce new drugs, and create genetic improvements.
Due to the similarities between the transmission of information in communication systems and the transmission of drugs in the human body, [12-15], several transmission platforms and models are used to deliver drugs only to specific targets to minimize the side effects are discussed. These specialized transmission systems, which are called drug delivery systems, could be used in the medical treatment of cancer, HIV, genetic diseases, gastrointestinal diseases, and neurological diseases. The routes of transmission (i.e., administration) of drugs into the body include oral ingestion, injection, and skin application [12].
The studies mentioned above have applied the key features of each system to the other. In biological systems, the evolutionary process used by living organisms over billions of years [5] and characteristics such as energy efficiency, biocompatibility, the ability to work in an aqueous medium, and pervasiveness are the most important features [16]. On the other hand, in digital systems, performance and efficiency are the two most important features [1]. Both systems have common challenges; attenuation, delay, interference, noise, and information loss could result in fatal communication problems. For instance, failure in biological systems could result in lethal diseases, such as cancer, in human beings [17]. However, biological communication (or molecular communication) is a promising scientific field. Its application to medical treatment could significantly improve human life quality; for instance, conventional therapies could access small and delicate body sites in a non-invasive way [18].
3. RESULTS
3.1. Gene Expression and Protein Delivery as a Digital Communication System
3.1.1. The Cell Nucleus as Biological Data Terminal Equipment (DTE)
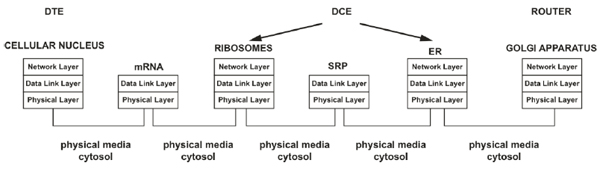
From our previous work [1], we suppose that the cellular nucleus behaves as a biological DTE, and then the nucleus represents the transmitter that contains the information source composed of nucleotide blocks called genes. This biological information must be processed intracellularly or extracellularly. We use long-distance cellular communication (exhibited, for example, in the endocrine system) [1, 19, 20] to propose our end-to-end digital system from a biological communication paradigm. Biologically a gene commonly is defined as a set of nucleotides that stores the information required for accomplishing a function (by a protein or ribonucleic acid (RNA)) [21] to be performed at a destination. Supported by our previous work [1], we hypnotized that the contents of a gene can be understood as an address at the network layer. The transmission of genes from the nucleus cell to the destination begins with the transcription process in which DNA information is copied into RNA.
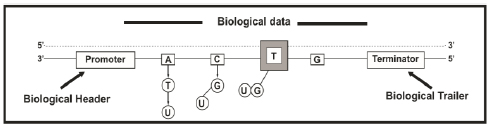
The DNA molecules contain digital information since it is encoded by four discrete values (four nucleotides). The nucleotides are nucleic acids monomers (DNA and RNA) comprising one nitrogenous base, a five-carbon sugar (deoxyribose in DNA and ribose in RNA), and at least one phosphate group. Adenine (A), thymine (T), cytosine (C), guanine (G), and uracil (U) are included in the nitrogenous bases. The DNA double helix comprises nucleotides containing the bases A, T, C, and G [22] and preserves its structure due to the complementarity between the nitrogenous bases of each strand of the helix [23] (i.e., the affinity of adenine to thymine and that of cytosine to guanine) [24]. As the information in DNA is divided into blocks of nucleotides called genes [25, 26] that possess start and termination sequences, then we can interpret that biological information is divided into data segments [1]. In packet-switching networks, digital information is divided into smaller units known as packets to facilitate processing. Therefore, a digital network packet may be analogous to a gene in a biological communication network [1].
At the beginning of transcription, the molecular motor RNA polymerase II (the RNAP II enzyme) recognizes a region of the promoter region's DNA sequence [27]. The promoter hosts the start sequence, which is when RNAP II begins to add nucleotides to create a complementary messenger RNA (mRNA) sequence. During transcription initiation, RNAP II produces a complementary single-stranded mRNA copy of one of the two DNA strands. The only difference between RNA and DNA is that RNAP II uses uracil (U) instead of thymine (T) during this process [28, 29]. There is no need to copy both DNA strands because the strands are exact complements. Moreover, this biological process resembles digital data compression because the same amount of data is contained in a smaller space [1]. In fact, the maximum compression of the genetic code for the optimal use of its nucleotides is given by H(pv) / log2a [30], where H(pv) is the entropy of the probability vector pv concerning a specific nucleotide, and a is the number of letters in an alphabet; in this case, the alphabet consists of the four nucleotides as mentioned above.
The enhancer is another element of the DNA strand that controls the quantity of protein produced according to the amount of mRNA. Because the enhancer controls the amount of information sent to the receiver, this process may be understood as a flow control at the sender end [1]. Data-link layers are responsible for flow control to ensure that a rapid sender cannot swamp a slow receiver with more messages than can be processed [31]. Transcription proceeds unidirectionally along with one of the DNA strands from the 5'P to the 3'OH of the deoxyribose phosphate backbone. This order is essential to ensure that the genetic information is copied appropriately; similarly, in digital communications, for example, the order lsb (less significant bit) or msb (most significant bit) is fundamental; precisely, in a serial transmission, the lsb generally is the first sent [1].
The halt of transcription is accomplished when an appropriate finalization sequence is recognized by RNAP II. [32]. In the primary transcript molecule (i.e., pre-mRNA) occurs the following modifications (maturation): (i) Splicing, (ii) Capping, and (iii) Polyadenylation [33]. The information added during capping and polyadenylation may be equivalent to the delimiting data flags used in digital communication systems, such as headers and trailers that encapsulate the information in the data-link layer in protocol hierarchies in network software (Fig. 1) [1, 4]. These flags are used for processing and error control [32]; concomitantly, with the utilization of digital flags, the previously mentioned maturations provide stability (control and posterior processing) to the mRNA molecules and prevent the degradation of the mRNA by enzymes in the cytosol (intracellular fluid), hence allowing the molecules to advance to the subsequent phases of biological processing [1].
The mechanical transport of mRNA molecules through the cytosol may be analogous to the transmission of information in wired communications (physical layer task) [1, 19, 24, 32].

3.1.2. The Ribosomes and Endoplasmic Reticulum (ER) as Biological Data Communication Equipment (DCE)
The transcription process is permitted to copy the biological information from DNA to RNA; this is necessary because DNA molecules cannot leave the cell's nucleus. Hence, at this point, the DTE must transmit the biological data to DCE through a physical interface (as in conventional communications systems). In our case, the cytosol may represent the physical interface (Fig. 2) [1].
In a digital communication system, the DCE (codec or modem) is the device required to format the information transmitted through a communication channel adequately. In our previous work [1], we consider that the ribosomes and ER represent the biological DCE because, through these organelles, the genetic information acquires a functional structure (or format when referring to data) that is later released into the biological communication channel and ultimately arrives at the biological receiver [1]. During translation, the “appropriate formatting” of biological data occurs when the information is converted into amino acid chains to obtain functionality inside and outside the cell. Thus, the biological DCE processes (codifies) information via translation and provides a specific input sequence (data in mRNA) that is associated with a specific output (sequence of amino acids); from the digital systems perspective, this type of codification process corresponds to conventional codification [1]. As in every state of the biological processes, throughout the translation, the mother nature has established the opportune addressing; therefore, the mRNA that leaves the nucleus has an implicit adjacent address that is comparable to a data link layer address to facilitate communication within a direct range of communication [1, 32]; therefore, the mRNA is bound by the ribosomes in the cytosol or those associated with the rough ER (RER). The transmission (movement) of biological information from the nucleus to the ribosomes or ER through the cytosol represents the arriving and moving of information into a biological communication channel, which is considered a task at the physical layer [1, 32].
Ribosomes, which are structures that serve as molecular motors, read the information contained in the biological sequence using a codon system (a codon is a triplet of nucleotides) [1, 27]. In the ribosome, the codons in the mRNA are recognized by transfer RNAs (tRNAs) that possess an anticodon (a sequence complementary to a particular codon) associated with a unique amino acid that binds specifically to the molecular structure of that tRNA.
Protein synthesis occurs in the ribosome through the signaling of tRNAs that indicate to the ribosomes the beginning (start codon) and end (stop codon) of the process to ensure the proper reading of the biological information [24]. From a digital perspective, the analysis of amino acid interactions that form proteins is essential for understanding the evolutionary relationships among organisms, developing new drugs, and producing synthetic proteins [12]. In a digital communication paradigm, the start and stop codons may correspond to synchronism signals. Synchronism between the source and destination is performed in synchronous transmissions through a start flag. In this type of information transmission, the transmitter sends the data, and the receiver must collect and process the data. The stop codon in biological signaling may be equivalent to the stop flag in synchronous communications that is used at the destination to indicate the end of the communication. We emphasize synchronous transmissions (and not asynchronous transmissions) because the transmission of a large amount of information is accomplished through synchronous communications; for instance, 1 gram of single-stranded DNA can encode 455 EB of data [34]. The signals to start and stop DNA translation allow the biological clocks present in cells to provide feedback during cellular processes [1, 32]. Because the processing of specific amino acids generates proteins (i.e., polypeptide chains), the order of the amino acids depends on the prior amino acid; therefore, this biological characteristic may correspond to input in Markov's source. Proteins consist of 20 different amino acids; therefore, the kth-order entropy is [1]:
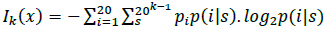
where pi is the probability of finding the ith amino acid, and p(i|s) is the conditional probability of the ith amino acid to occur after the amino acid string s [1, 19].
If all codons (amino acids) occur with an equal probability, the number of possible sequences (nps) in polypeptide chains of length N can be calculated as:
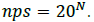
Because many amino acids do not have the same probability, Eq. (2) must be modified. Thus, if we consider a long sequence of N symbols selected from an alphabet of either codons or amino acids, we can determine the probability of that sequence as follows:
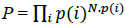
where N.p(i) is the probability of the ith symbol [30]. Considering the logarithm at both sides in (3),
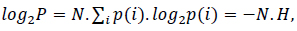
where
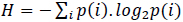 is the information or Shannon's entropy of the probability space containing the events i. Accordingly, the probability of obtaining a long sequence of N independent symbols or events from a finite alphabet is P = 2−N H, and the number of sequences of length N is nearly 2N H.
is the information or Shannon's entropy of the probability space containing the events i. Accordingly, the probability of obtaining a long sequence of N independent symbols or events from a finite alphabet is P = 2−N H, and the number of sequences of length N is nearly 2N H.
To define an end-to-end digital communication system supported in the biological behavior of gene expression, we have decided to analyze the production of proteins (e.g., peptide hormones, such as insulin) processed in the ER because many of these types of proteins have a role outside the cell, where they reach the receiver and complete an end-to-end communication. To obtain the mentioned types of proteins is mandatory to tag them (i.e., tagging to play a role outside the cell). Thus, a signal recognition particle (SRP) is bound to the amino acid sequence, thereby providing an implicit adjacent address via molecular tagging. This molecular tag is comparable to a data link layer address that facilitates communication within a direct communication range [1, 32].
The principal SRP task is to allow the nascent protein to arrive at a channel protein in the ER that oversees the translocation of the protein within the ER. Then, the SRP detaches from the protein and is recycled in the cytosol [1, 22]. Correspondingly, after the processing information and control information are used in digital communication systems, they are discarded. At this point, inside the ER, the proteins are folded and acquire the functional three-dimensional structure required for them to accomplish their specific biological functions [22] (equivalent to digital information after processing by the DCE, i.e., having the appropriate format) [1].
In biological systems, information errors can occur during DNA transcription and translation; similarly, in conventional communication systems, errors can occur in the transmission medium. Errors in cellular processing and information communication are responsible for many medical disorders, such as cancer, autoimmunity, and diabetes [19]. Supported by our previous study [1], Fig. (3) presents a layered network model of the transcription and translation of DNA from the typical network perspective. The structure of a layered model decomposes a large-scale system into a set of smaller units (i.e., layers) that are functionally independent of each other and specifies the interactions among the layers [32, 35]. Hence, an advantage of using a stack of layers is the fundamental use of the data link layer to transform an imperfect channel into a line free of transmission errors or report unsolved problems to the upper layer [1, 36]. Therefore, the application of such a model to biological systems (e.g., drug delivery) could provide high reliability [1].
3.1.3. The Golgi apparatus (GA) as an Internet (Border) Router
When proteins are functional, the RER transfers the proteins via molecular motors to the GA. Because each protein contains an implicit adjacent address via molecular tagging, which is comparable to a data link layer address that facilitates communication within a direct range of communication [1, 4], [32], the proteins are routed to the appropriate intercellular destinations; however, the GA determines whether the proteins remain inside the cell [22]. During this process, the proteins and their information content move from the RER to the GA, where the information is deposited into vesicles that bind the cis GA face. Then, new vesicles containing the protein information are generated, and other cellular components required for processing the proteins are added. The new vesicles deposit their contents into the medial GA face, and, again, new vesicles containing the protein and the elements necessary for further processing are formed. Finally, the vesicles reach the trans GA face, where a process identical to the previously defined process occurs; thus, the proteins are inserted into new vesicles but are directed to the endoplasmic membrane to be secreted outside the cell.
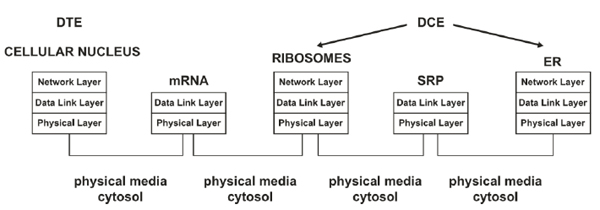
The GA's mentioned functions are comparable to those conducted by a border router in a network, as illustrated in the topology presented in Fig. (4). A router decides whether the information resides inside the network or leaves the network; thus, routing and routed processes are essential for sending information to the appropriate destination. Furthermore, the actions of depositing proteins, forming vesicles, and attaching information to specify a protein destination are analogous to those required in the processing of protocol data units (PDUs) in the router's layers [1].
The layered network model of the communication of information from the DTE to the GA is illustrated in Fig. (5). It represents gene expression as an intranet with its corresponding internet (border) router [1].
The usefulness of the digital theories that have been applied to the current biological analysis could be significant for the treatment of diseases because the proteins transmitted from the sender end, which correspond to the gene expression regulation, define the development of multicellular organisms, such as humans, and may cause the growth of pathological abnormalities, such as cleft palate or cancer [37]. Thus, gene expression regulation could be considered a flow control mechanism in digital communications.
3.1.4. Binary Representation of Gene Expression
A four-letter alphabet encodes genetic information; each letter of this alphabet corresponds to a nucleotide base. On the other hand, the amino acid alphabet consists of 20 separate letters, one for each amino acid. Consequently, based on information theory, the quantity of information carried by a single nucleotide base is 2 bits
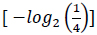 , and the quantity of information required to specify one amino acid from a set of 20 unambiguously is 4.3 bits
, and the quantity of information required to specify one amino acid from a set of 20 unambiguously is 4.3 bits
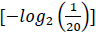 . Accordingly, using 6 bits to define an amino acid signifies an excess of information; nevertheless, this excess information capacity may explain the genetic code's redundancy [38]. In digital communication systems, redundancy represents a mechanism to control the information and identify errors. Likewise, the genetic code carries redundant information to diminish errors in gene expression [13, 36, 39].
. Accordingly, using 6 bits to define an amino acid signifies an excess of information; nevertheless, this excess information capacity may explain the genetic code's redundancy [38]. In digital communication systems, redundancy represents a mechanism to control the information and identify errors. Likewise, the genetic code carries redundant information to diminish errors in gene expression [13, 36, 39].
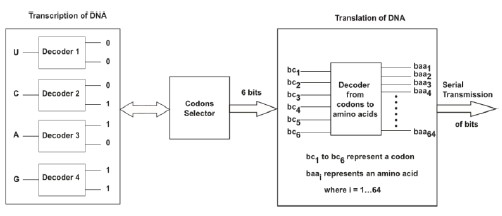
Different mixtures might be used to encode a nucleotide base with two bits. In this study, the method used in the study [40] is applied. The digital encoding method separates purine bases (R, adenine, or guanine) from pyrimidine bases (PY, uracil, or cytosine). In the pyrimidine and purine bases, the difference in the number of heterocyclic rings is noticeable. It means that the transition mutations preserving this classification compared with the transversion mutations changing the base classification are less damaging and frequent. In order to reflect the molecular similarities indicated by the nucleotides, binary identifiers are chosen. Table 1 shows the encoded nucleotide bases. This coding system keeps 0 and 1 as the first bit for the PY bases (two heterocyclic rings) and the R bases (one heterocyclic ring), respectively. Meanwhile, the second bit can be again 0 and 1, where “0” means the “weak” bases that form 2 hydrogen bonds with each other during Watson-Crick pairing (W=U or A), and “1” represents the “strong” bases that form 3 hydrogen bonds (S=C or G). We can eventually see the digital encoding of the nucleotide bases in this format [40]: U 00, C 01, A 10, and G 11.
Tables 2 and 3 show the standard amino acid's corresponding entries in the form of 6-bits binary messages. It means that these 6-bits are representative of the excellent correspondence of the basic unit of mRNA (codons) to protein translation. For proper protein folding, function, and clustering of amino acids with similar physicochemical, individual bit positions correlate with particular amino acid properties, such as size, hydropathy, and charge. First, the most “determinative” bits are considered by the clustering system mentioned above. The system then designates the corresponding nucleotide molecular features prioritized by nature; As an example, thymine can be replaced with uracil in this system. Furthermore, the amino acid corresponding to each codon, reflecting the long-established notion, has been illustrated in Tables 2 and 3.
In each codon, the second letter denotes the primary information regarding the intended amino acid, followed by the first letter. Therefore, vertical columns show related amino acids as in the same groups. The third letter of a codon usually does not modify the encoded amino acid; hence it is corrupt. Thus, to prioritize the most significant bits, a classification system is used that reorders in 2, 1, 3 the nucleotides in a codon. Table 2 depicts the binary representation employing the codon AUG, which codes for the amino acid methionine.
| - | PY (Pyrimidine: First bit is represented as 0) |
R (Purine: first bit is represented as 1) |
|---|---|---|
| W (Weak: second bit is represented as 0) |
U00 | A10 |
| S (Strong: second bit is represented as 1) |
C01 | G11 |
The 6-bit index of the codon is determined by concatenating the 2-bit identifiers from the second nucleotide (U00), the first nucleotide (A10), and the third nucleotide (G11) in order, yielding 001011. This method is equivalent to the following series of questions: Is the second base a purine? (0 for No, 1 for Yes). Is the second base strong? (0 for No, 1 for Yes). These questions are repeated for the first base of the codon and then for the third base of the codon [40]. Through this method, each of the 64 codons is assigned a unique 6-bit index that first places the most valuable information. A complete amino acid correspondence table generated using this method is provided in Table 3 [40]. To transmit biological information associated with gene expression from a digital communication perspective (i.e., to emulate DNA transcription in the biological DTE discussed in Section III-A), we use the method outlined in the previous paragraphs to associate each nucleotide base with 2 bits. Subsequently, to emulate DNA translation by initially processing the specific triplets of nucleotides discussed in Section III-B, we use a codon selector (Fig. 6) to obtain six bits representing each specific codon. Then, to complete the translation process, it is necessary to associate these 6 bits with the digital equivalence of an amino acid i.e., an entry in Table 3; thus, we used a digital decoder of 6 bits to 64 bits (Fig. 6).
| Bit 1 | Bit 2 | Bit 3 | Bit 4 | Bit 5 | Bit 6 |
|---|---|---|---|---|---|
| Is the | Is the | Is the | Is the | Is the | Is the |
| second base R? | second base S? | first base R? | first base S? | third base R? | third base S? |
| No | No | Yes | No | Yes | Yes |
| 0 | 0 | 1 | 0 | 1 | 1 |
| U00 | A10 | G11 | |||
| A | U | G | |||
| Methionine | |||||
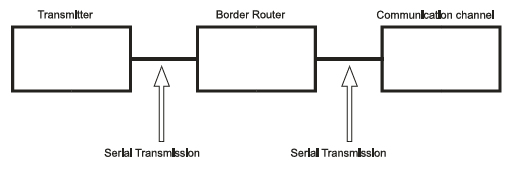
The genetic code utilizes three nucleotides (codon) to denote a specific amino acid [41]; this fact supports using a decoder with 64 outputs to define an amino acid. The reason behind this type of codification is that there are 20 amino acids; thus, it is necessary to classify the four nucleotides into groups of at least 3 to encode all 20 amino acids in 64 feasible combinations (i.e., 43 = 64 because 42 = 16 is not sufficient to encode 20 amino acids) [22]. As previously discussed (see Sections 3.1.2 and 3.1.3), after biological information is processed in biological DCE, the information travels to the GA, from which it is transmitted to the transmission channel (i.e., the bloodstream). Hence, we used serial communication to transmit each decoded bit individually to an internet (border) router, and from this router, the information was transmitted to the transmission channel, which was also performed using serial communication (Fig. 7).
3.1.5. Protein Delivery through a Communication Channel according to Shannon's Theorem
The mode of protein delivery to different destinations in the body is not the same in all cases and depends on the specific requirements of the system involved (e.g., the endocrine system). Hence, we consider cases in which the proteins secreted by the cell (e.g., hormones of a proteinaceous nature) move through the bloodstream (physical transmission medium - active random with drift transport) to a target organ (address destination). This type of molecular communication is referred to as intercellular communication (i.e., distances in the range of mm to m) [1, 20]. Thus, the movement of molecules in a fluid medium with drift (e.g., the bloodstream) is characterized as follows:
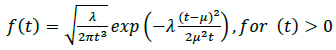
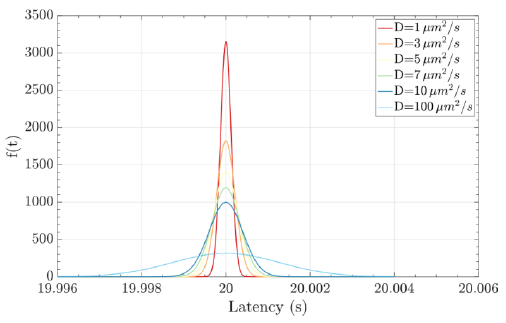
where the mean is µ = d / v, the shape parameter is λ = d2 / 2D, the velocity of the fluid medium is v ≥ 0, the diffusion coefficient is D (e.g., the typical diffusion coefficient of a protein molecule in water is D = 100µ2 / s), and the distance from the transmitter to the receiver is d. Fig. (8) illustrates an example of a hormonal signaling communication in which the transmitter is the pituitary glands cells, and the receiver is the thyroid glands cells [4, 7, 42, 43].
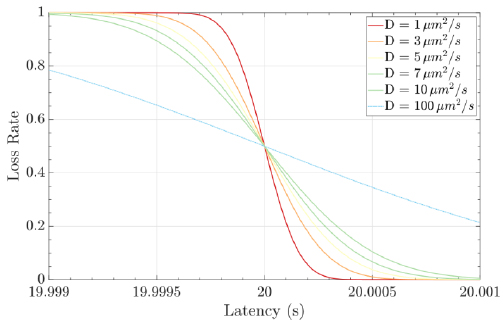
Molecular communications systems and typical communication systems can face difficulties during the transmission of information via communication channels. Specifically, in molecular communication, these issues include biochemical, thermal, and physical noise (due to the stochastic nature) [44] ; interference, which can be controlled by an appropriate transmission rate; and attenuation, which depends on the distance traveled and the physical characteristics of the fluid medium [1, 4]. The resulting damage to the signal information can cause latency (i.e., movement delay), which is expressed as d / v (20 seconds for the case represented in Fig. 8), jitter (i.e., variation in latency), which mathematical expression is D.d / 2.v3, and the loss rate (i.e., the probability that a molecule transmitted by a biological sender is not received by the intended biological receiver) can increase. The mathematical expression for the loss rate is
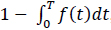 , which assumes that the receiver waits for the time duration T (Fig. 9) [1, 7].
, which assumes that the receiver waits for the time duration T (Fig. 9) [1, 7].
| First Base | - | - | - | - | - | Second Base | - | - | - | - | - | Third Base | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | U | - | - | C | - | - | A | - | - | G | - | - |
| U | UUU UUC UUA UUG |
0 1 10 11 |
Phe Phe Leu Leu |
UCU UCC UCA UCG |
10000 10001 10010 10011 |
Ser Ser Ser Ser |
UAU UAC UAA UGG |
100000 100001 100010 110011 |
Tyr Tyr Stp |
UGU UGC UGA UAG |
110000 110001 110010 100011 |
Cys Cys Stp Trp |
U C A G |
| C | CUU CUC CUA |
100 101 110 |
Leu Leu Leu |
CCU CCC CCA |
10100 10101 10110 |
Pro Pro Pro |
CAU CAC CAA |
100100 100101 100110 |
His His Gln |
CGU CGC CGA |
110100 110101 110110 |
Arg Arg Arg |
U C A |
| CUG | 111 | Leu | CCG | 10111 | Pro | CAG | 100111 | Gln | CGG | 110111 | Arg | G | |
| A | AUU AUC AUA |
1000 1001 1010 |
Ile Ile Ile |
ACU ACC ACA |
11000 11001 11010 |
Thr Thr Thr |
AAU AAC AAA |
101000 101001 101010 |
Asn Asn Lys |
AGU AGC AGA |
111000 111001 111010 |
Ser Ser Arg |
U C A |
| AUG | 1011 | Met | ACG | 11011 | Thr | AAG | 101011 | Lys | AGG | 111011 | Arg | G | |
| G | GUU GUC GUA |
1100 1101 1110 |
Val Val Val |
GCU GCC GCA |
11100 11101 11110 |
Ala Ala Ala |
GAU GAC GAA |
101100 101101 101110 |
Asp Asp Glu |
GGU GGC GGA |
111100 111101 111110 |
Gly Gly Gly |
U C A |
| GUG | 1111 | Val | GCG | 11111 | Ala | GAG | 101111 | Glu | GGG | 111111 | Gly | G | |
In this biological scenario, similar to conventional digital communication systems (e.g., network communication systems), digital communication theories could overcome the transmission troubles in the channel. Therefore, applying the previously mentioned digital techniques to gene expression could convert the proposal in this article into a real solution for the analyzed biological case. Hence, an advantage of using a layers’ stack is the fundamental use of the data link layer to transform a deficient channel into a line free of transmission errors or report unsolved problems to the upper layer [1, 36, 45].
Considering the communicational parameters that indicate the issues that can arise in a communication channel with noise, the maximum biological information transfer speed (capacity of a channel) is determined by the Shannon theorem as [45-47]:
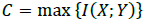
where I(X; Y) defines the entropy of the mutual information (MI) of X and Y. The information signals at the transmission and reception ends are denoted as X and Y, respectively. Fig. (10) illustrates the result of applying the Blahut-Arimoto algorithm to maximize the MI. Through this process, the biological transmitter emits a particle in each transmission slot. Also, in Fig. (10), the MI (measured in bits) is displayed concerning the fluid's diffusion constant and velocity or drift. The velocity-diffusion plot can be roughly divided into the following three regions [45-47]: (i) a diffusion-dominated region in which the MI is relatively insensitive to the velocity; (ii) a high-velocity region in which the MI is insensitive to the diffusion coefficient; and (iii) an intermediate region in which the MI is highly sensitive to both the velocity and diffusion coefficient of the medium. Besides, the MI increases as the velocity increases and reaches its maximum value at log2(N), where N is the number of transmission slots. If a transmitter does not send any molecule in any transmission slot, then the maximum value of MI will be log2(N + 1). It is also evident that when the velocity values are high, the MI values are independent of diffusion coefficient changes [45-47].
As the diffusion coefficient is a measure of the propagation time's uncertainty, the MI is expected to be lower with a significant diffusion coefficient, which is the case at great velocities. However, surprisingly, a higher diffusion coefficient ends in a higher MI at low velocities since, at low velocities, the diffusion in the medium enhances the molecule propagation from the transmitter to the receiver. Thus, to improve the MI at low velocity and low diffusion coefficients, it is necessary to release multiple molecules at one time. Using this method, the simultaneous transmission of various molecules (identical or different) is possible due to the lineal channel properties [42], [48-50]. From a networking perspective, the channel capacity is comparable to a flow control mechanism.
3.1.6. Use of Information at the Receiver
In the human body, the communication of biological information from a transmitter to a receiver is done through the bloodstream (in the example used in our research), and a target cell, tissue, or organ performs a physiological function. The transmitter sends the information using the data stored in the DNA molecules and at the destination can recognize the target cell, tissue, or organ. On the other side, in terms of the type of proteinaceous hormone involved, the receiver processes the information received. Here, we briefly describe a case in which this processing is performed through ligands and their receptors.
Ligands can be considered as signals attached to the receptors on the surface of a receiver. The signals from other receptors are then amplified and integrated by the receptors, and the resulting signals are transmitted to the destination cell. The following four features characterize the signal transduction processed by the receiver's communication architecture: specificity, amplification, desensitization, and integration [19].
The specificity determines the affinity between ligands and receptors at the receiver end. Specific ligands attach to specific (or complementary) receptors. Specificity is related to the signal molecule that matches its complementary molecular receptor. As a concept in the network, specificity can be used as an addressing mechanism when in Ethernet networks and at the data link layer level, a broadcast is sent to recognize an Internet Protocol (IP) address. In this case, all devices in the network could receive the broadcast message, but it will be processed by the device whose MAC matches its IP address [1, 36].
The increase in the strength of the signal is called amplification. In this physiological phase of biological processing, the response to the first signal activates a second signal, the response to the second signal causes the activation of a third signal, and so on. From a network perspective, this cell function is similar to the function of internetwork devices (i.e., switches, routers, among others.) that amplify the received signal before it is processed [51].
The capacity to eliminate the signal once received is an action of desensitization. The sensitivity of receptor systems is the function by which the signal is attenuated after a certain threshold period (i.e., the receiver becomes insensitive to the signal). After this threshold period, the receiver becomes sensitive again. This process may be comparable to the network case mentioned previously because when a computer receives a broadcast with an IP that does not match its own, the computer ignores the information, but if a new broadcast is sent, the computer processes it [1, 36].
The ability to appropriately interpret and incorporate the received signal with other signals is named Integration. Integration is defined as a system's capacity to receive multiple signals and assemble a unified response appropriate to the cell or organism's needs. In Sections 3.1.4 and 3.1.5, we examined how the transmission of biological data (represented by bits) is sent into the channel bit by bit separately due to the transmission channel's linear properties. In the mentioned case, all internetwork device receivers can process various input signals simultaneously [36]. Thus, the simultaneous processing of received signals at the destination in digital communication systems and biological systems may be analogous.
Like digital communication systems, the receiving of biological information through receptors can be described by discrete states, i.e., bound (B) or unbound (U). In the U state, the receptor waits for the arrival of molecular information; once the information arrives, it enters the B state. In the B state, the receptor cannot receive other molecular information (rendering it insensitive to the signal), and a certain amount of processing time is required before the receptor returns to the U state [52].
This binding process can be represented by a discrete-time Markov chain using steps of length Δt and a state transition probability matrix (at the ith step as follows) [52]:
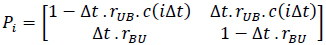
where rUB·C(iΔt) is the transition rate from U to B, which is proportional to the ligand concentration C(iΔt) and the transition rate from B to U is rBU, which is independent of the ligand concentration.
In equation (7), if ci = c(i Δt), αci = ΔtrUB c(i Δt) and β = ΔtrUB, Pi becomes,
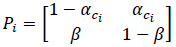
where αci is the transition probability from U to B, which is sensitive to the input ligand concentration ci, and β is the transition probability from B to U, which is transition insensitive. If we consider the extreme ligand concentration from the minimum allowed concentration ci = L to the maximum allowed concentration ci = H, the signal transduction process is a time-inhomogeneous Markov chain according to either (9) or (10).
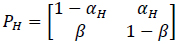
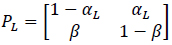
The choice of (9) or (10) is determined by the ligand concentration [52].
In the biological process described, the membrane protein behaves as a transducer that decodes the received signal (DCE), triggering several reactions inside the target cell, tissue, or organ of the body (DTE) [53]. This behavior is comparable to the function performed at the receiver end in digital communication systems to process information that will be profitable at the destination.
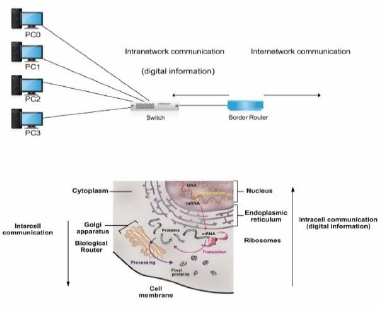
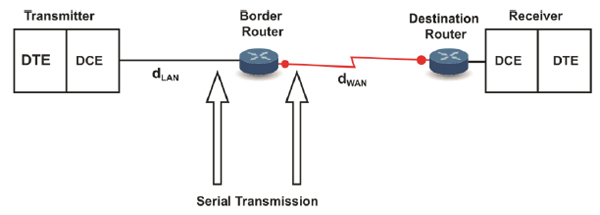
As previously mentioned and according to the internetwork communication characteristics discussed throughout this article, the gene expression of proteins could be considered an internet in which the intracellular communication at the transmitter end emulates a LAN network in which the distance from the ER to the GA (dLAN in Fig. 11) is 2µm. We do not consider in dLAN the distance between the ribosomes and ER because the ribosomes that participate in the translation process are found in the cytosol and RER; therefore, this distance is not fixed. However, if this distance could be considered dLAN, it would still represent a biological LAN cover distance because it represents an intracellular distance [4].
Alternatively, the transmission of proteinaceous hormones could be defined as a WAN network (Fig. 11) because it covers a distance dWAN (in the range of mm to m) [20,42].
The receiver end also emulates a LAN network with a cover distance of up to the size of a cell (approximately 100µm) [4].
Similar to typical networks, the biological WAN covers a more significant distance than the biological LANs [54]. Besides, similar to the conventional networks, the biological LANs are interconnected by routers [55] (Fig. 11). Hence, at the transmitter end, the GA acts as a biological router (see Section 3.1.3). We consider that the receiver end, i.e., the target organ, also behaves as a router because among a set of receivers that are likely destinations connected by a common transmission channel (i.e., the bloodstream), the receivers for which the information is intended (i.e., with the suitable addressing) react to the received information. Once again, the described case may be equivalent to Ethernet networks in which a broadcast is sent through the transmission channel (with a logical bus topology) to each computer in the network, but only the computer with the appropriate IP address processes the received communication. Therefore, the end-to-end addressing could be comparable to the network addressing at the network layer [1].
Once the target cell receives the biological data, the information is communicated to other organelles using an implicit adjacent address that is comparable to the data link layer address used to facilitate communication within a direct range of communication [1,32]. The received biological message is physically transmitted to the target cell.
Fig. (12) presents an end-to-end layered network model of the gene expression of proteins [1] from the typical network perspective of gene expression as an internet. The structure of a layered model decomposes a large-scale system into a set of smaller units (i.e., layers) that are functionally independent of each other and specifies the interactions among the layers. One advantage of a stack of layers is the fundamental use of the data link layer to transform an imperfect channel into a line that is free of transmission errors or report unsolved problems to the upper layer [36] therefore, the application of such a model to biological systems (e.g., drug delivery) is highly reliable [1].
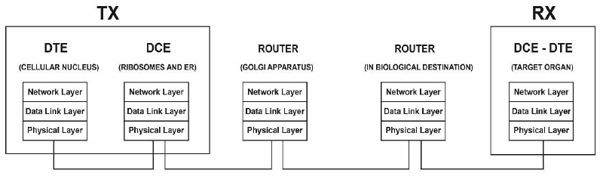
4. DISCUSSION
Molecular Communication (MC) is a promising research area for novel applications, especially toward early diagnosis and treatment of diseases using Information and Communication Technology (ICT), such as artificial organs, continuous health monitoring, lab-on-a-chip, and intelligent drug delivery. It conveys an expressive potential as a choice to traditional wireless communications, especially in those situations where the latter may collapse, such as intrabody medium and restrained channels such as pipe networks. MC is a bio-inspired communication method that uses molecules to encode, transmit, and receive information in the same way the living cells communicate. MC is intrinsically biocompatible, energy-efficient, and robust in physiological circumstances. Thus, nano communications currently focus on the ICT analysis of nucleic acids (i.e., DNA and RNA) due to their biocompatible and chemical stability, especially in in-body applications. Nucleotide Shift Keying (NSK) encodes the information into the base sequences of DNAs. For instance, through NSK, over 200 MB data files were encoded and stored by using more than 13 million nucleotides. On top of everything else, the application of NSK in DNA-based MC may raise the ordinary low data rates of molecular communications to the extent of competing with conventional wireless communication standards because of the high DNA information density. Hence, NSK can facilitate indoor artificial molecular wireless communications with data rates up to hundreds of Mbps, leading to an innovative communication paradigm, molecular information fidelity (Mi-Fi). In Mi-Fi, multiuser channel access can be achieved through Molecular Division Multiple Access (MDMA) capability, i.e., communicating via multiple types of information-carrying molecules, e.g., various DNA strands, at once [56].
4.1. Bio-hybrid Medical Treatments
The analysis of gene expression as a digital communication system specifically from a network perspective, could be applied to bio-hybrid medical treatments that inject delicate and expensive drugs (not toxic) into the human body. In these cases, equation (6) describes the highest quantity of the drug (i.e., C) according to the bloodstream velocity (v) and the physical conditions of the blood (D) (Fig. 10). The slots in it could be considered periods during which the injected particles (i.e., bits) are transmitted. Similarly, in regular communications, if the transmission rate is ≤ C, there is a high probability that the information will be received adequately at the destination (target organ) through a noisy channel (such as the bloodstream). Notably, the proposed applications may provide certain advantages in controlling drug arrival over the typical transport of drugs, in which the dosage cannot be adjusted after ingestion. Thus, characteristics, such as addressing and flow control, could be adjusted to deliver drugs to their desired locations at a controlled rate and dosage (depending on their toxicity level) while minimizing the drug's effects on the healthy parts of the body.
Hence, patients could be more comfortable, the risks related to medical errors could be reduced, and the cost-effectiveness of these drugs relative to that of conventional drugs could be increased. Moreover, the proposed application could benefit from nanotechnology applications, which have enabled the development of microneedles, which are tiny needles that enter the skin without stimulating the nerves [12, 57].
4.2. Hormone Therapy Management
It consists of the administration and adequate transmission of precise amounts of hormones to avoid considerable side effects during the treatment of diseases, such as cancer [13]. Thus, the mechanisms, such as addressing, flow control, error control, traffic control and Shannon's theorem that were used to design the layered network model of the transmission of proteinaceous hormones in the endocrine system to a target organ may be used in hormone therapy because these network theories could act only in specific target organs (i.e., destination addressing), provide the appropriate dose (i.e., flow control, error control, traffic control, and Shannon's theorem) and avoid side effects thanks to a higher targeting accuracy (i.e., addressing).
CONCLUSION
We model the gene expression through a digital communication system. In this model, the transmitter side comprises the cell nucleus carrying DNA as a source of information (data terminal equipment, DTE) and both the ribosomes and the endoplasmic reticulum as data communications equipment (DCE). The bloodstream is modeled as a noisy transmission channel, in which Shannon's theorem establishes the maximum biological information transfer velocity (spread of hormones in the endocrine system). We corroborated that successful transmission can occur even though the propagation channel is noisy or has restrictions with values lower or equal to the maximum information transfer rate. On the receiver side, hormone target cells (acting as DCE) capture the biological information and decode the received signal, producing multiple biochemical reactions within the cell or target organ (acting as DTE) to accomplish a biological function in the body. The introduced digital communication model could be employed in the medical field to represent biological systems' functioning. The benefits of digital systems impact the processing and transmission of information positively. Consequently, the proposed model represents a new path for treating lethal diseases and the comprehensive improvement of humans' quality of life through high-level medical treatments with non-aggressive or collateral effects.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No humans and animals were used for studies that are the basis of this research.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
This work was supported by the Universidad Nacional de Chimborazo under project Modelamiento Comunicacional de la Expresión Genetica como un Sistema de Transmisión Digital, Res. Nº 33-CIV-10-03-2020.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


