All published articles of this journal are available on ScienceDirect.
Modeling and Methods of Statistical Processing of a Vector Rhytmocardiosignal
Abstract
Aims:
We have developed a new approach to the study of human heart rate, which is based on the use of a vector rhythmocardiosignal, which includes as its component the classical rhythmocardiosignal in the form of a sequence of heart cycle durations in an electrocardiogram.
Background:
Most modern automated heart rate analysis systems are based on a statistical analysis of the rhythmocardiogram, which is an ordered set of R-R interval durations in a recorded electrocardiogram. However, this approach is not very informative, since R-R intervals reflect only the change in the duration of cardiac cycles over time and not the entire set of time intervals between single-phase values of the electrocardiosignal for all its phases.
Objective:
The aim of this paper is to present a mathematical model in the form of a vector of stationary and permanently connected random sequences of a rhythmocardiosignal with an increased resolution for its processing problems. It shows how the vector rhythmocardiosignal is formed and processed in diagnostic systems. The structure of probabilistic characteristics of this model is recorded for statistical analysis of heart rate in modern cardiodiagnostics systems.
Methods:
Based on a new mathematical model of a vector rhythmocardiosignal in the form of a vector of stationary and permanently connected random sequences, new methods for statistical estimation of spectral-correlation characteristics of heart rate with increased resolution have been developed.
Results:
The spectral power densities of the components of the vector rhythmocardiosignal are justified as new diagnostic features when performing rhythm analysis in modern cardiodiagnostics systems, complementing the known signs and increasing the informative value of heart rate analysis in modern cardiodiagnostics systems.
Conclusion:
The structure of probabilistic characteristics of the proposed mathematical model for heart rate analysis in modern cardiodiagnostics systems is studied. It is shown how the vector rhythmocardiosignal is formed, and its statistical processing is carried out on the basis of the proposed mathematical model and developed methods.
1. INTRODUCTION
The heart rate analysis has long been an integral part of not only modern cardiology but also many other areas of biometrics because the heart rate is a carrier of information about consistency and order in the functioning of the human body as an integral system. In particular, the analysis of heart rate makes it possible to assess the overall activity of regulatory mechanisms of the body, mechanisms of neurohumoral regulation of the heart, the relationship between the sympathetic and parasympathetic parts of the autonomic nervous system, as well as the psycho-emotional state of a human. In addition, the heart rate analysis is carried out for early diagnosis of the pathological condition of the fetus, the state of the autonomic system in diabetic patients. Heart rate makes it possible to assess the value of the risk of death in myocardial infarction, the degree of tension of the state of the regulatory process in the human body, etc [1-12].
The special efficiency of the heart rate analysis is achieved by using modern computerized diagnostic systems that make it possible to automate the assessment of diagnostic signs and make medical decisions about the human heart rate based on recorded cardiosignals, mainly electrocardiosignals. The accuracy, reliability, information content and speed of functioning of cardiodiagnostic computerized heart rate research systems significantly depend on the adequacy and constructiveness of the mathematical model of heart rate, as well as the accuracy, reliability, information content, speed of methods and algorithms of its analysis in these information systems.
Most methods for processing the classical rhythmocardiosignal in the framework of the stochastic approach are based on three of its probabilistic models, namely, a random variable, a random stationary sequence, and a periodically correlated random sequence are used. These models are based on an approach to describing the heart rate as a sequence of R-R intervals that uses a ritmocardiogram (classical ritmocardiogram), which imposes significant limitations on the informative value of heart rate analysis. The essence of this limitation is that the values of R-R intervals, which are the corresponding values of the rhythmocardiogram, reflect only the change in the duration of cardiac cycles over time, and not the entire set of time intervals between single-phase values of the electrocardiosignal for all its phases, which does not make it possible to describe the heart rate with sufficient information. That is why the approach based on the analysis of the classical rhythmocardiogram as a sequence of R-R intervals does not allow us to identify more subtle and detailed features of the heart rate in modern computer systems of medical diagnostics.
In the study [13, 14], a new approach to heart rate analysis based on a high-resolution rhythmocardiosignal was developed. As indicated in these works, the classical rhythmocardiogram is embedded in a rhythmocardiogram with increased resolution, which is the basis for increasing the level of the information content of heart rate analysis in modern computer systems for functional diagnostics of the human heart state based on a rhythmocardiosignal with increased resolution.
In this approach, the heart rate was represented by a high-resolution rhythmocardiosignal (other names: high-informative rhythmocardiosignal or vector rhythmocardiosignal), the mathematical model of which was a vector of normally distributed random variables. Therefore, the classical ritmocardiogram is embedded in a ritmocardiogram with increased resolution, which is the basis for the level increase of information content of heart rate analysis in the modern computer systems for functional diagnostics of the human heart state based on a ritmocardiosignal with increased resolution.
As a mathematical model of a rhythmocardiosignal with increased resolution, in the study [13, 14], is justified the use of a vector of random variables with a normal distribution. This stochastic model can already take into account several phases of the cardiac cycle when analyzing the heart rate. However, this model is a relatively simple mathematical model of a high-resolution rhythmocardiosignal, since it does not allow us to study its temporal dynamics. To take into account the temporal dynamics of a rhythmocardiosignal with increased resolution, it is necessary to use the mathematical apparatus of random sequence theory, namely, to consider it a vector of discrete random sequences.
In this paper, a mathematical model of a rhythmocardiosignal with an increased resolution for its processing problems is described as a vector of stationery and stationary connected random sequences. It shows how the vector rhythmocardiosignal is formed, processed and modeled in diagnostic systems. The structure of probabilistic characteristics of this model is recorded for statistical analysis of heart rate in modern cardiodiagnostics systems.
2. MATERIALS AND METHODS
2.1. Electrocardiosignal Mathematical Model in the form of a Conditional Cyclic Random Process
Let's move on to constructing a mathematical model of a vector rhythmocardiosignal. Since the rhythmocardiosignal is formed from an electrocardiosignal, the mathematical model of the vector rhythmocardiosignal is based on the corresponding model of the electrocardiosignal itself (ECS). According to the study [15], a mathematical model of an electrocardiosignal that is conditional cyclic random process is called a process  , which is given on the cartesian product of two stochastically independent probabilistic spaces with sets of elementary events Ω and Ω' on the set of real numbers R, and for which the following conditions are met:
, which is given on the cartesian product of two stochastically independent probabilistic spaces with sets of elementary events Ω and Ω' on the set of real numbers R, and for which the following conditions are met:
1) There is such a random function  , what for each ω', appropriate ω'-realisation Tω' (t,n) of this function satisfies the conditions of the rhythm function;
, what for each ω', appropriate ω'-realisation Tω' (t,n) of this function satisfies the conditions of the rhythm function;
2) For each ω' із Ω' finite-dimensional vectors 

 -multiple separabilities of the process
-multiple separabilities of the process  , with all the goals k
, with all the goals k N is stochastically equivalent in a broad sense;
N is stochastically equivalent in a broad sense;
3) For any different  random processes
random processes  are isomorphic to the order and values cyclic random processes.
are isomorphic to the order and values cyclic random processes.
Realisation of (ω'-realisation) a random function T(ω', t, n) there is a deterministic function Tω'(t, n), which satisfies the conditions of the rhythm function, namely:
a group of conditions:
a)  ;
;
b)  ;
;
c)  for any t1
for any t1 R and t2
R and t2 R, for which t1 < t2, for the function Tω'(t,n) a strict inequality is fulfilled
R, for which t1 < t2, for the function Tω'(t,n) a strict inequality is fulfilled  ;
;
3) The function Tω'(t,n) is the smallest in modulus  among all such functions
among all such functions  , which satisfy the above conditions 1 and 2.
, which satisfy the above conditions 1 and 2.
2.2. A Generalized Mathematical model of a High-resolution Rhythmocardiosignal
The conditional cyclic random process ξ(ω,ω',t) allows simultaneous consideration of both the stochasticity of the morphological structure of electrocardiosignals (which is important for their statistical morphological analysis), as well as the stochasticity of their rhythmic structure (which is important for the heart rate analysis). Considering that according to such a mathematical model of the electrical signal, information about the heart rate is contained in the rhythm function T(ω',t,n) of the conditional cyclic random process ξ(ω,ω',t), and also taking into account the fact that the processing of electrocardiosignals is carried out in a digital system, the analysis of heart rate is reduced to the statistical analysis of the random rhythm function  of the conditional cyclic random process discrete argument
of the conditional cyclic random process discrete argument 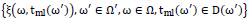 .
.
Random rhythm function T(tml(ω'),n) is completely defined by the elements of the random domain D(ω') according to the formula:
 |
(1) |
When n = 1, rhythm function T(tml(ω'),1) is calculated in the following way:
 |
(2) |
For each ω'-realisation Dω' =  of the random domain definition Dω' =
of the random domain definition Dω' =  of the conditional cyclic random process of a discrete argument that is given on a probabilistic space (Ω′, F′, P′), the following conditions apply:
of the conditional cyclic random process of a discrete argument that is given on a probabilistic space (Ω′, F′, P′), the following conditions apply:  , whetherm2 < m1, or whetherm2 = m1, and l2 < l1, in other cases
, whetherm2 < m1, or whetherm2 = m1, and l2 < l1, in other cases 
 .
.
If to base the heart rate analysis on a random rhythm function T(tml(ω'),1) the conditional cyclical random process ξ(ω, tml,(ω')), preserving a tight bind to the phase of the cardiac cycle and the number of the cardiac cycle, a mathematical model of the rhythmocardiosignal with increased resolution is presented as a vector of random sequences:
 |
(3) |
where each l-component of a vector is a random sequence Tl(ω',m), the value of which is equal to the value of the random rhythm function T(tml(ω'),1) at moments in time tml(ω') from a discrete set  . The set of Dl(ω') is integrated into the D(ω') and describes the time distances between the same type l - phases of the studied electrocardiosignal in its two adjacent cycles, namely:
. The set of Dl(ω') is integrated into the D(ω') and describes the time distances between the same type l - phases of the studied electrocardiosignal in its two adjacent cycles, namely:
 |
(4) |
Dimension (the number of components) L of vector  determines the resolution of the rhythmocardiosignal and is equal to the number of studied time intervals between pre-selected phases in the electrocardiosignal, which can be identified by segmentation and detection methods when solving the problem of automatic formation of the rhythmocardio signal from the electrocardiosignal [16-28]. According to the block diagram shown in Fig. (1), the first block is the determination of the same type of phases corresponding to the boundaries of segments-zones ECS; this stage is implemented on the basis of the use of methods for segmenting cyclic signals. Detection of the same type of phases within certain zones is the next step in the formation of a vector rhythmocardiosignal. At this stage, information is obtained about time points that correspond to the maximum or minimum of characteristic ECS segments, for example, R, P, or T. The final stage in this structure is the formation of a vector rhythmocardiosignal based on the information obtained at the previous stages.
determines the resolution of the rhythmocardiosignal and is equal to the number of studied time intervals between pre-selected phases in the electrocardiosignal, which can be identified by segmentation and detection methods when solving the problem of automatic formation of the rhythmocardio signal from the electrocardiosignal [16-28]. According to the block diagram shown in Fig. (1), the first block is the determination of the same type of phases corresponding to the boundaries of segments-zones ECS; this stage is implemented on the basis of the use of methods for segmenting cyclic signals. Detection of the same type of phases within certain zones is the next step in the formation of a vector rhythmocardiosignal. At this stage, information is obtained about time points that correspond to the maximum or minimum of characteristic ECS segments, for example, R, P, or T. The final stage in this structure is the formation of a vector rhythmocardiosignal based on the information obtained at the previous stages.

2.3. Updated Mathematical Model of a High-resolution Rhythmocardiosignal and its Probabilistic Characteristics
Let's move on to the justification of the probabilistic characteristics of the vector  of random sequences. One of the simplest stochastic models that can take into account the dynamics of changes in the rhymocardiosignal with increased resolution is the vector
of random sequences. One of the simplest stochastic models that can take into account the dynamics of changes in the rhymocardiosignal with increased resolution is the vector  =
=  f the stationary and stationery-related random sequences. First of all, note that the vector
f the stationary and stationery-related random sequences. First of all, note that the vector  of the stationary and stationary-related random sequences, in the partial case, if its components are stationary sequences with independent values, i.e. white noises given on a set of integers, is a well-known model of a rhythmocardiosignal with increased resolution in the form of a random variable vector, which was developed in the studies. However, the hypothesis of independence or uncorrelation of rhythmocardiosignal readings does not correspond to the reality on practise, which requires taking into account the stochastic relationship between rhythmocardiosignal readings with increased resolution, and therefore the use of a more complex and more general mathematical model in the form of a vector
of the stationary and stationary-related random sequences, in the partial case, if its components are stationary sequences with independent values, i.e. white noises given on a set of integers, is a well-known model of a rhythmocardiosignal with increased resolution in the form of a random variable vector, which was developed in the studies. However, the hypothesis of independence or uncorrelation of rhythmocardiosignal readings does not correspond to the reality on practise, which requires taking into account the stochastic relationship between rhythmocardiosignal readings with increased resolution, and therefore the use of a more complex and more general mathematical model in the form of a vector  stationary and stateonery -related random sequence
stationary and stateonery -related random sequence
Let's move on to substantiating the probabilistic characteristics of the vector  random sequences. One of the simplest stochastic models that takes into account the dynamics of changes in the rhymocardiosignal with increased resolution is the vector
random sequences. One of the simplest stochastic models that takes into account the dynamics of changes in the rhymocardiosignal with increased resolution is the vector  stationary and stationary connected random sequences. First of all, we note that the vector
stationary and stationary connected random sequences. First of all, we note that the vector  stationary and stationary-related random sequences, in the partial case, if its components are stationary sequences with independent values white noises given on a set of integers, this is a well-known model of a rhythmocardios signal with increased resolution in the form of a random variable vector, which was developed in [29, 30]. However, in practice, the hypothesis of independence or uncorrelation of rhymtocardiosignal readings does not correspond to reality, which requires taking into account the stochastic relationship between rhymtocardiosignal readings with increased resolution, and therefore the use of a more complex and more general mathematical model in the form of a vector
stationary and stationary-related random sequences, in the partial case, if its components are stationary sequences with independent values white noises given on a set of integers, this is a well-known model of a rhythmocardios signal with increased resolution in the form of a random variable vector, which was developed in [29, 30]. However, in practice, the hypothesis of independence or uncorrelation of rhymtocardiosignal readings does not correspond to reality, which requires taking into account the stochastic relationship between rhymtocardiosignal readings with increased resolution, and therefore the use of a more complex and more general mathematical model in the form of a vector  stationary and stationary possible random sequences.
stationary and stationary possible random sequences.
Defining property of the vector  stationary and permanently connected random sequences are the invariance of its family of distribution functions to time shifts by an arbitrary integer k
stationary and permanently connected random sequences are the invariance of its family of distribution functions to time shifts by an arbitrary integer k Z. For any distribution function F
Z. For any distribution function F of order
of order  іfrom the family of vector distribution functions
іfrom the family of vector distribution functions  for stationary and permanently connected random sequences the following equality holds:
for stationary and permanently connected random sequences the following equality holds:
 |
(5) |
Distribution function  in the case when l1 = l2 = ... = lp = l is a distribution function
in the case when l1 = l2 = ... = lp = l is a distribution function  stationary components
stationary components  of vector
of vector  - that is an automatic order distribution function p for a stationary random sequence
- that is an automatic order distribution function p for a stationary random sequence  , what describing the time distances between single-phase readings of an electrocardiosignal for its l- phase. If p = 1, then we will have a one dimensional
, what describing the time distances between single-phase readings of an electrocardiosignal for its l- phase. If p = 1, then we will have a one dimensional  automatic distribution function of a stationary random sequence
automatic distribution function of a stationary random sequence  .
.
In the case where equality l1 = l2 = ... = lp = l if the distribution function is not executed  is a compatible distribution function for several (at least two) stationary vector components
is a compatible distribution function for several (at least two) stationary vector components  , which describes the time distances between single-phase readings of an electrocardiosignal as a whole for its different phases.
, which describes the time distances between single-phase readings of an electrocardiosignal as a whole for its different phases.
Family of vector distribution functions  stationary and stationary connected sequences most fully describe its probabilistic structure, but methods for statistical estimation of the distribution function
stationary and stationary connected sequences most fully describe its probabilistic structure, but methods for statistical estimation of the distribution function  they are too bulky for their practical use in computer diagnostic systems of the functional state of the cardiovascular system of the human body. Therefore, in addition to the vector distribution functions
they are too bulky for their practical use in computer diagnostic systems of the functional state of the cardiovascular system of the human body. Therefore, in addition to the vector distribution functions  effective is the use of instantaneous order functions
effective is the use of instantaneous order functions  , which, if they exist, are also invariant to time shifts (shifts by argument m).
, which, if they exist, are also invariant to time shifts (shifts by argument m).
So, if there is a mixed initial moment function  of order
of order  of stationary and stationary connected random sequences, then the equality holds for it:
of stationary and stationary connected random sequences, then the equality holds for it:
 |
(6) |
where M - operator of mathematical expectation.
If there is a mixed central moment function  of order
of order  of stationary and permanently connected random sequences, then the equality holds for it:
of stationary and permanently connected random sequences, then the equality holds for it:
 |
(7) |
where is the plural  is a set of first-order initial moments (mathematical expectations) of stationary random sequences from the set
is a set of first-order initial moments (mathematical expectations) of stationary random sequences from the set  .
.
In practice, to analyze a rhythmocardiosignal with increased resolution, it is appropriate to use mixed moment functions of low orders, namely, mixed initial moment functions of the second-order – covariance functions and mixed central moment functions of the second-order – correlation functions. In this case, the initial moment functions of the second order for the vector  stationary and permanently connected random sequences are represented as a matrix of covariance functions:
stationary and permanently connected random sequences are represented as a matrix of covariance functions:
 |
(8) |
what can be noted more compactly like this:
 |
(9) |
where each of its elements is a covariance function  , which is set as:
, which is set as:
 |
(10) |
Since the components of the vector  random sequences are stationary and permanently connected sequences, then their covariance functions are functions of only one integer argument u, which is equal to u = m1-m2. Therefore the covariance matrix of this random vector can be represented as follows:
random sequences are stationary and permanently connected sequences, then their covariance functions are functions of only one integer argument u, which is equal to u = m1-m2. Therefore the covariance matrix of this random vector can be represented as follows:
 |
(11) |
where each of its elements is a covariance function  which is equal to:
which is equal to:
 |
(12) |
Provided that  , covariance function
, covariance function  it is an auto-variational function l stationary components
it is an auto-variational function l stationary components  of vector
of vector  which describes the time distances between single-phase readings of an electrocardiosignal for its lphase. If
which describes the time distances between single-phase readings of an electrocardiosignal for its lphase. If  , then the covariance function
, then the covariance function  is a mutual covariance function for two stationary vector components
is a mutual covariance function for two stationary vector components  which describe the time distances between single-phase electrocardiosignals for l1 and l2 phase.
which describe the time distances between single-phase electrocardiosignals for l1 and l2 phase.
Mixed second-order central moment functions for a vector  stationary and stationary connected random sequences are represented as a matrix of correlation functions:
stationary and stationary connected random sequences are represented as a matrix of correlation functions:
 |
(13) |
which can be written more compactly like this:
 |
(14) |
where each of its elements is a correlation function  , which is set as follows:
, which is set as follows:
 |
(15) |
Since the components of the vector  random sequences are stationary and stationary connected sequences, then their correlation functions are functions of only one integer argument u, which is equal to u = m1-m2. Therefore the correlation matrix of this random vector can be represented as:
random sequences are stationary and stationary connected sequences, then their correlation functions are functions of only one integer argument u, which is equal to u = m1-m2. Therefore the correlation matrix of this random vector can be represented as:
 |
(16) |
where each of its elements is a correlation function  , which is equal to:
, which is equal to:
 |
(17) |
If l1 = l2 = l, are correlation function  is an autocorrelation function l-stationary components
is an autocorrelation function l-stationary components  of vector
of vector  , which describes the time distances between single-phase readings of an electrocardiosignal for its l -phase. If
, which describes the time distances between single-phase readings of an electrocardiosignal for its l -phase. If  , then the correlation function
, then the correlation function  is a mutual correlation function for two stationary components of the vector
is a mutual correlation function for two stationary components of the vector  which describe the time distances between single-phase electrocardiosignals for l1 and l2 phase.
which describe the time distances between single-phase electrocardiosignals for l1 and l2 phase.
2.4. Statistical Estimates of Probabilistic Characteristics of a High-resolution Rhythmocardiosignal
Let's write down the formula expressions for calculating the implementations of statistical estimates of probabilistic characteristics of a rhythmocardiosignal with increased resolution. The formula expression for calculating the implementation of a statistical estimate  of covariance function
of covariance function  of two stationary and stationary-related random sequences
of two stationary and stationary-related random sequences  , which describe the time distances between single-phase electrocardiosignals for
, which describe the time distances between single-phase electrocardiosignals for  - of it phases, namely:
- of it phases, namely:
where M - the number of recorded complete cycles of the electrocardiosignal from which the rhythmocardiosignal with increased resolution is formed, M1 (M1 << M) is the maximum value of arguments m1, m2 which is selected depending on the number of averages in the implementation of statistics to ensure the required level of accuracy and reliability of statistical evaluation.
 |
(18) |
If in the formula (18) p = 1, then l1 = l2 =...= lp = l, then we get an expression for calculating the implementation of a statistical estimate  of the initial moment s -order
of the initial moment s -order  of the stationary random sequence
of the stationary random sequence  , namely:
, namely:
 |
(19) |
If in the formula (19) s = 1, then we get an expression for calculating the implementation of a statistical estimate  of the initial moment of the first order
of the initial moment of the first order  (mathematical expectation) of a stationary random sequence
(mathematical expectation) of a stationary random sequence  , namely:
, namely:
 |
(20) |
The formula expression for calculating the implementation of a statistical estimate of the correlation function  of two stationary and stationary-related random sequences
of two stationary and stationary-related random sequences  and
and  , which describe the time distances between single-phase electrocardiosignals for l1 and l2- phases, namely:
, which describe the time distances between single-phase electrocardiosignals for l1 and l2- phases, namely:
 |
(21) |
Since for stationary and stationary-related random sequences, the correlation functions are the functions of only one integer argument u, which is equal to u = m1 - m2, then their statistical estimates also depend on only one argument u. In this case, if we assume the ergodicity of the stationary components of the vector, then the formula (21) looks like this:
 |
(22) |
If in the formula (22) u = 0, then l1 = l2 = l, then we have the expression for calculating the implementation of the variance estimate of the stationary random sequence  , namely:
, namely:
 |
(23) |
In order to reduce the number of diagnostic signs for a high-resolution rhythmocardiosignal it is necessary to take into account the fact of symmetry  of the estimated matrix of correlation functions
of the estimated matrix of correlation functions  , which indicates the adequacy evaluation of only those elements of the matrix
, which indicates the adequacy evaluation of only those elements of the matrix  , which lie on its diagonal and above the diagonal, namely, such an ordered totality
, which lie on its diagonal and above the diagonal, namely, such an ordered totality  On the diagonal of this matrix, when l1 = l2, estimates of autocorrelation functions are placed, and the elements of matrix
On the diagonal of this matrix, when l1 = l2, estimates of autocorrelation functions are placed, and the elements of matrix  , which are placed above its diagonal, namely, when l1 = l2, are estimates of inter-correlation functions. Therefore, the matrix
, which are placed above its diagonal, namely, when l1 = l2, are estimates of inter-correlation functions. Therefore, the matrix  , without losing its information content, can be replaced with a triangular matrix
, without losing its information content, can be replaced with a triangular matrix  .
.
Another way to reduce the number of diagnostic features in information systems for the analysis of heart rate for the main rhythmocardiosignals with increased resolution is to use spectral decompositions of the triangular matrix elements themselves  in particular, by using the discrete Fourier transform of autocorrelation estimates and inter-correlation functions from this matrix. Namely, instead of a triangular matrix
in particular, by using the discrete Fourier transform of autocorrelation estimates and inter-correlation functions from this matrix. Namely, instead of a triangular matrix  of the correlation functions a triangular matrix can be used the elements of which are Fourier images of the corresponding estimates of the correlation functions from the matrix
of the correlation functions a triangular matrix can be used the elements of which are Fourier images of the corresponding estimates of the correlation functions from the matrix  . Namely, Fourier images from The Matrix
. Namely, Fourier images from The Matrix  are calculated like this:
are calculated like this:
 |
(24) |
Based on Bessel's inequality, we will not choose the entire set as diagnostic signs  function counts
function counts  , but only a certain subset of their first ones M2 (M2 << M1) of counts
, but only a certain subset of their first ones M2 (M2 << M1) of counts  which contribute to the full energy of evaluation
which contribute to the full energy of evaluation  of the correlation function not less than 95%.
of the correlation function not less than 95%.
3. RESULTS AND DISCUSSION
Based on the above mathematical model and methods of processing a high-resolution rhythmocardiosignal, a multifunctional software package for modeling and automated analysis of a wide class of cyclic heart signals for the needs of functional medical diagnostics has been upgraded. Namely, as a component of this software package, a system of computer programs has been developed for the automated formation and the statistical analysis of heart rate based on a vector rhythmocardiosignal (rhythmocardiosignal with increased resolution), which expanded the functionality of the existing software package and made it possible to automatically analyze the heart rate with increased information content. A typical structural and functional diagram of the software for processing ECS is shown in Fig. (2). A dashed line in this block diagram highlights the blocks that are emphasized in this article. The software package is implemented in the programming language Object Pascal.
According to the blocks presented in the block diagram, ECS processing includes evaluating the segmental structure using segmentation methods, for example [29]. Evaluation of the rhythm function by interpolating the rhythmic structure (discrete rhythm function), based on the method [30].
Further, the development of the ECS branches out into two stages (two problems are solved). The first stage performs morphological analysis, which, according to this structure, provides for statistical processing of ECS, normalization of statistical estimates and their decomposition in the Chebyshev basis, and decision-making based on the obtained morphological features. This stage is described in [31]. The second stage performs rhythm analysis and consists in forming a vector rhythmocardiosignal, statistical processing of the vector and spectral analysis of the obtained statistical estimates.
As an example, Fig. (3) shows a general view of the program interface for evaluating the autocorrelation function and the cross-correlation function of the components of a vector rhythmocardiosignal.


Figs. (4 and 5) show the stages of formation from the ECS vector rhytmocardiosignal, and Figs. (6 and 7) show the results of statistical processing of the rhytmocardiosignal with increased information content, by statistical evaluation of its corresponding statistical characteristics corresponding to the blocks of the structural and functional scheme 2.



 , component of the vector rhythmocardiosignal of the first component
, component of the vector rhythmocardiosignal of the first component  and the second component
and the second component  , that describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R - intervals of electrocardiosignal.
, that describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R - intervals of electrocardiosignal.

 component of the vector rhythmocardiosignal of the first component
component of the vector rhythmocardiosignal of the first component  and the second component
and the second component  , describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R - intervals of electrocardiosignal.
, describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R - intervals of electrocardiosignal.
Fig. (8) shows the results of the spectral decomposition of statistical estimates of the power spectral densities of the components of the vector rhythmocardiosignal.

 statistical estimates of autocorrelation functions
statistical estimates of autocorrelation functions  and
and  of the first component
of the first component  and the second component
and the second component  , what describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
, what describing the duration accordingly: a) P - intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
Fig. (5A) shows graphs of relative errors in the formation of high-resolution rhythmocardiogram samples corresponding to R–R intervals and obtained on the basis of the method of segmentation and detection of extreme values of electrocardiogram zones, based on Brodsky-Darkhovsky statistics (indicated on the graph with bold dots) and on the basis of the method based on the use of a first-order difference function (indicated on the graph with triangles). Fig. (5B) shows graphs of relative errors in the formation of high-resolution rhythmocardiogram samples corresponding to T–T intervals, and obtained on the basis of the method of segmentation and detection of extreme values of electrocardiogram zones, based on Brodsky-Darkhovsky statistics (indicated on the graph with bold dots) and on the basis of the method based on the use of a first-order difference function (indicated on the graph with triangles).
Analyzing the graphs of relative errors in the formation of a high-resolution rhrythmocardiogram, which are presented in Fig. (5), it can be argued that the method of automatic formation of a high-resolution rhrythmocardiogram, which is based on Brodsky-Darkhovsky Statistics, has higher accuracy compared to a similar method based on the use of a first-order difference function.
From the registered electrocardiogram according to the method of automatic formation of a rhythmocardiogram with increased accuracy, the implementation of  of four components of the vector
of four components of the vector 
 stationary and stationary related random sequences. The first component of
stationary and stationary related random sequences. The first component of  this vector is a random stationary sequence describing durations P in the electrocardiosignal for all its 245 recorded cycles. Second component
this vector is a random stationary sequence describing durations P in the electrocardiosignal for all its 245 recorded cycles. Second component  of this vector is a random stationary sequence describing durations R in the electrocardiosignal. Third component
of this vector is a random stationary sequence describing durations R in the electrocardiosignal. Third component  this vector is a random stationary sequence describing durations T in the electrocardiosignal. The fourth component
this vector is a random stationary sequence describing durations T in the electrocardiosignal. The fourth component  of this vector is a random stationary sequence describing durations R-R - intervals in the electrocardiosignal. As an example, the implementation schedule
of this vector is a random stationary sequence describing durations R-R - intervals in the electrocardiosignal. As an example, the implementation schedule  of the first component is shown in Fig. (6). A, and the implementation graph
of the first component is shown in Fig. (6). A, and the implementation graph  of the second component is shown in Fig. (6B).
of the second component is shown in Fig. (6B).
The justification of statistical hypotheses about the stationarity of the mathematical expectation and variance of the components of the vector rhythmocardiosignal have been tested. Namely, the statistical hypotheses about the invariance of the mathematical expectation and variance of the components of the vector rhythmocardiosignal have been tested by applying well-known statistical criteria for checking the equality of mathematical expectations and variances of two random variables represented by their samples (as a sample, two sections of each component of the vector rhythmocardiosignal were taken. The Student's criterion (for mathematical expectation of the vector rhrythmocardiosignal component) and Fischer's criterion (for variance of the vector rhrythmocardiosignal component) have been used as a statistical criterion for testing hypotheses about stationarity. The results of 13 of the 15 tests performed with a confidence level of 0.95 indicate the consistency of the hypothesis about the stationarity of the components of the vector rhythmocardiosignal, which can be considered verification of a new mathematical model of the rhythmocardiosignal with increased resolution in the form of a vector of stationary and stationary-related random sequences.
To check the stationary components of the vector for their normality, Fig. (7) shows histograms for implementations T1ω,(m), T2ω,(m) corresponding stationary vector components  .
.
 .
.| Stationary Component Number | Significance of Implementing a Statistical Estimate of Mathematical Expectation |
|---|---|
| 1 | C1T1 = 14,88 |
| 2 | C1T2 = 25,02 |
| 3 | C1T3 = 73,82 |
| 4 | C1T4 = 799,51 |

 statistical estimates of power spectral densities
statistical estimates of power spectral densities  of the first component
of the first component  and the second component
and the second component  , what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
, what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
To test the hypothesis of the normality of the distribution of stationary components of a random vector  according to the Pearson consent criterion, it has been found that these results do not contradict the hypothesis of the normality of its distribution. Normality of the vector distribution
according to the Pearson consent criterion, it has been found that these results do not contradict the hypothesis of the normality of its distribution. Normality of the vector distribution  is the basis for substantiating diagnostic features in systems for the analysis of heart rate using a high-resolution rhythmocardiogram within the framework of spectral correlation theory, which significantly reduces the computational complexity of such an analysis. In this case, to estimate the probabilistic structure of the vector
is the basis for substantiating diagnostic features in systems for the analysis of heart rate using a high-resolution rhythmocardiogram within the framework of spectral correlation theory, which significantly reduces the computational complexity of such an analysis. In this case, to estimate the probabilistic structure of the vector  stationary and stationary-related random sequences, it is sufficient to perform a statistical estimation of the only vector
stationary and stationary-related random sequences, it is sufficient to perform a statistical estimation of the only vector  of its mathematical expectations according to Formula (20) and the matrix of correlation functions
of its mathematical expectations according to Formula (20) and the matrix of correlation functions  according to the Formula (22).
according to the Formula (22).
Fig. (8) shows graphs of implementations  statistical estimates of autocorrelation functions
statistical estimates of autocorrelation functions  of the first component
of the first component  and the second component
and the second component  , what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
, what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
(Fig. 9) shows graphs of implementations  statistical estimates of power spectral densities
statistical estimates of power spectral densities  of the first component
of the first component  and the second component
and the second component  , what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
, what describing the duration accordingly: a) P- intervals of electrocardiosignal; b) R- intervals of electrocardiosignal.
The above implementations of statistical estimates of restorative probabilistic characteristics significantly complement the known informative features in the systems of the heart rate analysis. Namely, the new diagnostic features are being introduced into practice, such as the matrix of correlation functions and the matrix of spectral power densities of stationary components of the rhythmocardiosignal with increased resolution, which, by reflecting the stochastic temporal dynamics of the heart rate, make it possible to increase the level of information content of the heart rate analysis in modern cardiodiagnostic systems.
CONCLUSION
The paper presents a new mathematical model of a rhythmocardiosignal with increased resolution in the form of a vector of stationary and stationary-related random sequences, which, in comparison with the known mathematical models of heart rate, allows to increase the level of information content of automated heart rate analysis and is logically consistent with the stochastic mathematical model of an electrocardiosignal in the form of a conditional cyclic random process. The mathematical model of a high-resolution rhythmocardiosignal has been verified by testing the statistical hypotheses about stationarity for the normal distribution of components of a high-resolution rhythmocardiosignal, which has been the basis for reducing the computational complexity of statistical methods for the analysis of heart rate in computer systems of medical diagnostics.
The statistical methods for the analysis of high-resolution rhythmocardiosignals have been developed, which are based on their new mathematical model in the form of a vector of stationary and permanently connected random sequences, namely, expressions are recorded for calculating implementations of statistical estimates of the vector of mathematical expectations and a matrix of correlation functions of components of the vector of the rhythmocardiosignal. A number of new diagnostic features in computer systems of medical diagnostics based on vector rhythmocardiosignals for assessing the state of the cardiovascular system and adaptive-regulatory mechanisms of the human body as a whole have been justified. Namely, the known diagnostic features of the vector rhythmocardiosignal are supplemented with such new diagnostic features as the matrix of correlation functions and the matrix of spectral power densities of stationary components of the high-resolution rhythmocardiosignal, which by reflecting the stochastic temporal dynamics of the heart rate make it possible to increase the level of information content of heart rate analysis in modern cardiodiagnostic systems.
Based on the new mathematical model and methods developed in the dissertation for processing high-resolution rhythmocardiosignals, a multifunctional software package for modelling and automated analysis of a wide class of cyclic heart signals for the needs of functional medical diagnostics has been upgraded. Namely, as a component of this software package, a system of computer programs has been developed for automated formation and statistical analysis of heart rate based on a vector rhythmocardiosignal, which expanded the functionality of the existing software package and made it possible to perform heart rate analysis with increased information content automatically.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
AVAILABILITY OF DATA AND MATERIALS
Not applicable.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.


